题目内容
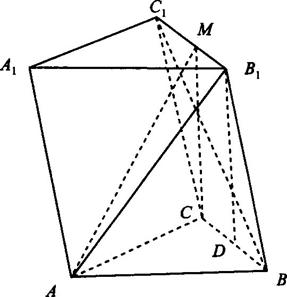
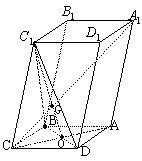
如图,已知斜四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD,
(1)证明:C1C⊥BD;
(2)当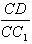 的值为多少时,能使A1C⊥平面C1BD?请给出证明。
的值为多少时,能使A1C⊥平面C1BD?请给出证明。
(1)证明:C1C⊥BD;
(2)当
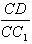 的值为多少时,能使A1C⊥平面C1BD?请给出证明。
的值为多少时,能使A1C⊥平面C1BD?请给出证明。 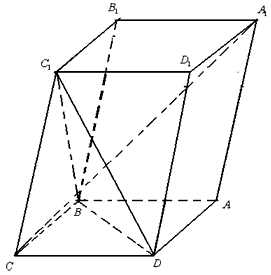
| 解:(1)连结A1C1、AC,AC和BD交于O,连结C1O, ∵ 四边形ABCD是菱形, ∴ AC⊥BD,BC=CD, 又∵∠BCC1=∠DCC1,C1C=C1C, ∴△C1BC≌△C1DC, ∴C1B=C1D, ∵DO=OB, ∴C1O⊥BD, 但AC⊥BD,AC∩C1O=O, ∴BD⊥平面AC1, 又C1C 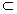 平面AC1, 平面AC1, ∴C1C⊥BD; |
 |
(2)当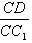 =1时,能使A1C⊥平面C1BD; =1时,能使A1C⊥平面C1BD;由(1)知,BD⊥平面AC1, ∵A1C 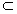 平面AC1, 平面AC1, ∴BD⊥A1C, 当 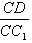 =1时,斜四棱柱的六个面是全等的菱形, =1时,斜四棱柱的六个面是全等的菱形,同BD⊥A1C的证法可得BC1⊥A1C; BD∩BC1=B, ∴A1C⊥平面C1BD。 |

练习册系列答案
相关题目
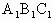 的底面是直角三角形,AC⊥CB,∠ABC=
的底面是直角三角形,AC⊥CB,∠ABC=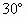 ,侧面
,侧面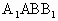 是边长为a的菱形,且垂直于底面,
是边长为a的菱形,且垂直于底面,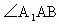 =
=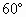 ,E、F分别是
,E、F分别是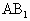 、BC的中点.
、BC的中点.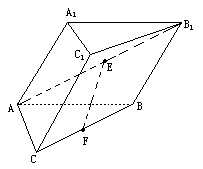
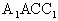 ;
;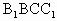 的体积;
的体积;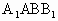 所成角的正切值.
所成角的正切值.