题目内容
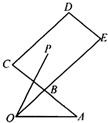如图，B是AC的中点，| BE |
| OB |
| OP |
| OA |
| OB |
①当x=0时，y∈[2，3]；
②当P是线段CE的中点时，x=-
| 1 |
| 2 |
| 5 |
| 2 |
③若x+y为定值1，则在平面直角坐标系中，点P的轨迹是一条线段；
④x-y的最大值为-1；
其中你认为正确的所有结论的序号为
分析：利用向量共线的充要条件判断出①错，③对；利用向量的运算法则求出
，求出x，y判断出②对．
| OP |
解答：解：对于①当
=y
，据共线向量的充要条件得到P在线段BE上，故1≤y≤3，故①错
对于②当当P是线段CE的中点时，
=
+
=3
+
(
+
)
=3
+
(-2
+
)=-
+
故②对
对于③x+y为定值1时，A，B，P三点共线，又P是平行四边形BCDE内（含边界）的一点，故P的轨迹是线段，故③对
故答案为②③④
| OP |
| OB |
对于②当当P是线段CE的中点时，
| OP |
| OE |
| EP |
| OB |
| 1 |
| 2 |
| EB |
| BC |
=3
| OB |
| 1 |
| 2 |
| OB |
| AB |
| 1 |
| 2 |
| OA |
| 5 |
| 2 |
| OB |
对于③x+y为定值1时，A，B，P三点共线，又P是平行四边形BCDE内（含边界）的一点，故P的轨迹是线段，故③对
故答案为②③④
点评：本题考查向量的运算法则、向量共线的充要条件．
练习册系列答案
优加精卷系列答案
相关题目
如图，在△ABC和△AEF中，B是EF的中点，AB=EF=2，CA=CB=3，若
如图，在Rt△ABC中，∠ACB=90°，AC=BC=4，D是AB中点，E是AC的中点，现将△ABC沿CD翻折成直二面角A-DC-B．
，P是平行四边形BCDE内（含边界）的一点，且
+
．有以下结论：
；
，P是平行四边形BCDE内（含边界）的一点，且
+
．有以下结论：
；