题目内容
已知球O的半径为4,圆M与圆N为该球的两个小圆,AB为圆M与圆N的公共弦,AB=4,OM=ON=a,则两圆的圆心距|MN|的最大值为( )
| A.3 | B.2 | C.3 | D.6 |
B
∵ON=a,球半径为4,
∴小圆N的半径为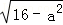 ,
,
∵小圆N中弦长AB=4,作NE垂直于AB,
∴NE=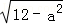 ,同理可得ME=
,同理可得ME=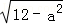 ,
,
在直角三角形ONE中,
∵NE=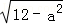 ,ON=a,
,ON=a,
∴OE=2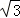 ,
,
∵ON⊥NE,OM⊥ME,所以O,M,E,N四点共圆
∴两圆的圆心距|MN|的最大值为2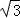
故选B.

∴小圆N的半径为
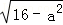 ,
,∵小圆N中弦长AB=4,作NE垂直于AB,
∴NE=
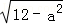 ,同理可得ME=
,同理可得ME=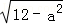 ,
,在直角三角形ONE中,
∵NE=
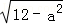 ,ON=a,
,ON=a,∴OE=2
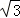 ,
,∵ON⊥NE,OM⊥ME,所以O,M,E,N四点共圆
∴两圆的圆心距|MN|的最大值为2
故选B.


练习册系列答案
相关题目
 :
: 的离心率为
的离心率为 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线 相切.
相切. 的切线
的切线 与椭圆相交于A、B两点,求证:以AB为直径的圆过原点.
与椭圆相交于A、B两点,求证:以AB为直径的圆过原点.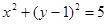 ,直线L:
,直线L: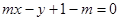 .
.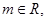 直线L与圆C总有两个不同交点;
直线L与圆C总有两个不同交点;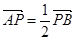 ,求此时直线L的方程.
,求此时直线L的方程.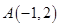 为圆心的圆与直线
为圆心的圆与直线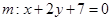 相切,过点
相切,过点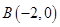 的动直线与圆
的动直线与圆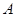 相交于
相交于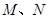 两点.
两点.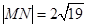 时,求直线
时,求直线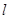 的方程.
的方程.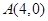 的直线
的直线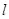 与曲线
与曲线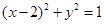 有公共点,则直线
有公共点,则直线 ,
,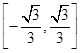
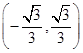
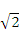 ,0)引直线ι与曲线
,0)引直线ι与曲线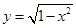 交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )
交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )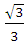 B.-
B.-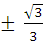 D-
D-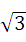
 轴上,半径长是
轴上,半径长是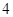 ,且与直线
,且与直线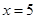 相切的圆的方程是 .
相切的圆的方程是 .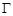 :
: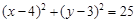 ,过圆
,过圆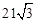
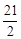
 中,直线
中,直线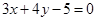 与圆
与圆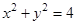 相交于A、B两点,则弦AB的长等于 ( )
相交于A、B两点,则弦AB的长等于 ( )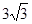 B.
B.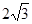 C.
C.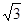 D.1
D.1