题目内容
(本小题满分12分)已知椭圆 :
: 的离心率为
的离心率为 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线 相切.
相切.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)已知圆M: 的切线
的切线 与椭圆相交于A、B两点,求证:以AB为直径的圆过原点.
与椭圆相交于A、B两点,求证:以AB为直径的圆过原点.
 :
: 的离心率为
的离心率为 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线 相切.
相切.(Ⅰ)求椭圆
 的方程;
的方程;(Ⅱ)已知圆M:
 的切线
的切线 与椭圆相交于A、B两点,求证:以AB为直径的圆过原点.
与椭圆相交于A、B两点,求证:以AB为直径的圆过原点.(Ⅰ)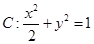 (Ⅱ)见解析
(Ⅱ)见解析
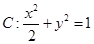 (Ⅱ)见解析
(Ⅱ)见解析(Ⅰ)由已知得,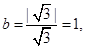
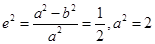 ,故
,故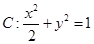 4分
4分
(Ⅱ)①当直线 的斜率不存在时.
的斜率不存在时.
因为直线 与圆M相切,故其中的一条切线方程为
与圆M相切,故其中的一条切线方程为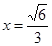 .
.
由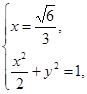 不妨设
不妨设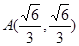 ,
,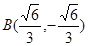 ,
,
则以AB为直径的圆的方程为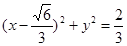 ,显然过原点
,显然过原点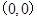 . 6分
. 6分
②当直线 的斜率存在时.
的斜率存在时.
设直线 的方程为
的方程为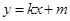 .因为直线
.因为直线 和圆M相切,所以圆心到直线
和圆M相切,所以圆心到直线 的距离
的距离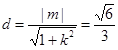 ,整理,得
,整理,得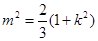 , ①
, ①
由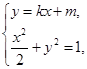 消去
消去 ,得
,得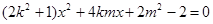 ,
,
所以设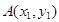 ,
,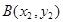 ,则
,则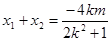 ,
,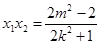 .
.
所以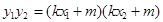
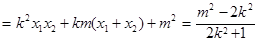 .
.
所以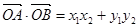
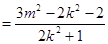 .②
.②
将①代入②,得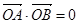 ,显然以AB为直径的圆经过定点O(0,0)
,显然以AB为直径的圆经过定点O(0,0)
综上可知,以AB为直径的圆过定点(0,0).(13分) 12分
【考点定位】本题考查椭圆的标准方程以及简单几何性质、圆的切线等基础知识,意在考查学生运用数形结合思想、转化与化归思想以及综合分析问题解决问题的能力以及运算能力.
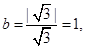
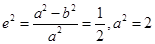 ,故
,故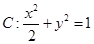 4分
4分(Ⅱ)①当直线
 的斜率不存在时.
的斜率不存在时.因为直线
 与圆M相切,故其中的一条切线方程为
与圆M相切,故其中的一条切线方程为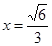 .
.由
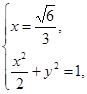 不妨设
不妨设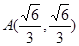 ,
,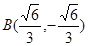 ,
,则以AB为直径的圆的方程为
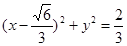 ,显然过原点
,显然过原点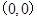 . 6分
. 6分②当直线
 的斜率存在时.
的斜率存在时.设直线
 的方程为
的方程为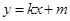 .因为直线
.因为直线 和圆M相切,所以圆心到直线
和圆M相切,所以圆心到直线 的距离
的距离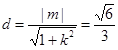 ,整理,得
,整理,得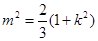 , ①
, ①由
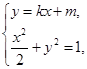 消去
消去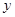 ,得
,得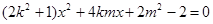 ,
,所以设
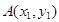 ,
,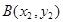 ,则
,则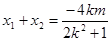 ,
,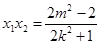 .
.所以
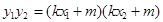
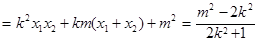 .
.所以
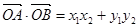
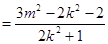 .②
.② 将①代入②,得
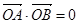 ,显然以AB为直径的圆经过定点O(0,0)
,显然以AB为直径的圆经过定点O(0,0)综上可知,以AB为直径的圆过定点(0,0).(13分) 12分
【考点定位】本题考查椭圆的标准方程以及简单几何性质、圆的切线等基础知识,意在考查学生运用数形结合思想、转化与化归思想以及综合分析问题解决问题的能力以及运算能力.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
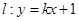 与圆
与圆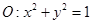 相交于
相交于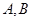 两点,则
两点,则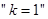 是“
是“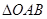 的面积为
的面积为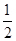 ”的( )
”的( ) 充分而不必要条件
充分而不必要条件  必要而不充分条件
必要而不充分条件  充分必要条件
充分必要条件  既不充分又不必要条件
既不充分又不必要条件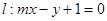 与圆
与圆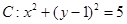 的位置关系是( ).
的位置关系是( ).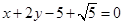 被圆
被圆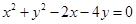 截得的弦长为 ( )
截得的弦长为 ( ) 关于( )
关于( ) 对称
对称 对称
对称 对称
对称  对称
对称
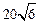





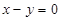 相切的圆的方程为____________________.
相切的圆的方程为____________________.