题目内容
如下图所示,在四棱锥
P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,E是AB上一点,PE⊥EC.已知 ,CD=2,
,CD=2, ,求:
,求:
(1)
异面直线PD与EC的距离;(2)
二面角E-PC-D的大小.
答案:略
解析:
解析:
|
(1) 以D为原点,
由已知可得 D(0,0,0), ,C(0,2,0),设A(x,0,0)(x>0),则B(x,2,0), ,C(0,2,0),设A(x,0,0)(x>0),则B(x,2,0), , , , , . .
由 PE⊥CE得 ,即 ,即 ,故 ,故 . .
由  ,得DE⊥CE,又PD⊥DE,故DE是异面直线PD与CE的公垂线,易得 ,得DE⊥CE,又PD⊥DE,故DE是异面直线PD与CE的公垂线,易得(2) 作DG⊥PC,垂足为G,可设G(0,y,z).由 得 得 ,即 ,即 ,故可取 ,故可取 . .
由  得 得 , ,
即  .又由F在PC上得 .又由F在PC上得 ,故m=1, ,故m=1,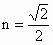 , , .因 .因 , , ,故平面E-PC-D的平面角θ的大小为向量 ,故平面E-PC-D的平面角θ的大小为向量 的夹角. 的夹角.
故  , , , ,
即二面角 E-PC-D的大小为 . . |

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目

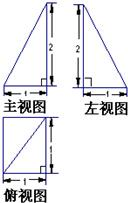 (理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1).
(理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1). ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.


 +1)a2
+1)a2 )a2
)a2