题目内容
如下图所示,在四棱锥
P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD, ,BC=1,PA=2,E为PD的中点.
,BC=1,PA=2,E为PD的中点.
(1)
求直线AC与PB所成角的余弦值;(2)
在侧面PAB内找一点N,使NE⊥面PAC,并求出点N到AB和AP的距离.
答案:略
解析:
解析:
|
(1) 建立如下图所示的空间直角坐标系,则A,B,C,D,P,E的坐标为A(0,0,0)、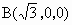 、 、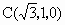 、D(0,1,0)、P(0,0,2)、 、D(0,1,0)、P(0,0,2)、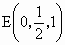 , ,从而
设  与 与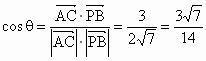 , ,
∴AC 与PB所成角的余弦值为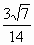 . .
(2) 由于N点在侧面PAB内,故可设N点坐标为(x,0,z),则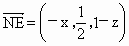 ,由NE⊥面PAC可得, ,由NE⊥面PAC可得,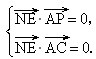 即 即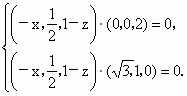
化简得 即 N点的坐标为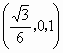 ,从而N点到AB和AP的距离分别为1, ,从而N点到AB和AP的距离分别为1, . . |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
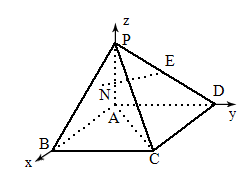
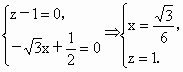
 (理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1).
(理)设6张卡片上分别写有函数f1(x)=x、f2(x)=x2、f3(x)=x3、f4(x)=sinx、f5(x)=cosx和f6(x)=lg(|x|+1). ,CD=2,
,CD=2, ,求:
,求:


 +1)a2
+1)a2 )a2
)a2