题目内容
为提高学生的素质,某校决定开设一批选修课程,分别为文学、艺术、竞赛三类,这三类课程所含科目的个数分别占总数的
、
、
,现在3名学生独立2从中任选一个科目参加学习.
(1)求他们选择的科目所属类别互不相同的概率;
(2)记ξ为3人中选择的科目属于文学或竞赛的人数,求ξ的分布列及数学期望.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
(1)求他们选择的科目所属类别互不相同的概率;
(2)记ξ为3人中选择的科目属于文学或竞赛的人数,求ξ的分布列及数学期望.
(0)∵甲、乙、丙六人选择的科目所属类别互不相同的情况有A33=6种,
∴他们选择的科目所属类别互不相同的概率p=6×
×
×
=
.
(2)设η为3人中选择的科目属于艺术的人数,则η~多(3,
),
由题设知ξ=3-η,
则P(ξ=k)=P(η=3-k)=
(
)3-k(0-
)&n多sp;k,
∴ξ人分布列是
Eξ=3-Eη=3-3×
=
.
∴他们选择的科目所属类别互不相同的概率p=6×
| 0 |
| 2 |
| 0 |
| 4 |
| 0 |
| 4 |
| 3 |
| 06 |
(2)设η为3人中选择的科目属于艺术的人数,则η~多(3,
| 0 |
| 4 |
由题设知ξ=3-η,
则P(ξ=k)=P(η=3-k)=
| C | 3-k3 |
| 0 |
| 4 |
| 0 |
| 4 |
∴ξ人分布列是
| &n多sp;ξ | &n多sp;0 | &n多sp;0 | 2&n多sp; | &n多sp;3 | ||||||||
| &n多sp;P | &n多sp;
|
&n多sp;
|
&n多sp;
|
&n多sp;
|
| 0 |
| 4 |
| 多 |
| 4 |

练习册系列答案
相关题目
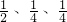 ,现在3名学生独立地从中任选一个科目参加学习.
,现在3名学生独立地从中任选一个科目参加学习.