题目内容
如图,在三棱柱ABC—A1B1C1中,AA1⊥面ABC,AC⊥BC,E、F分别在线段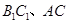 上,B1E=3EC1,AC=BC=CC1=4.
上,B1E=3EC1,AC=BC=CC1=4.
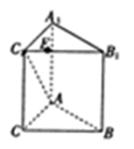
(1)求证:BC⊥AC1;
(2)试探究:在AC上是否存在点F,满足EF//平面A1ABB1,若存在,请指出点F的位置,并给出证明;若不存在,说明理由.
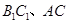 上,B1E=3EC1,AC=BC=CC1=4.
上,B1E=3EC1,AC=BC=CC1=4.
(1)求证:BC⊥AC1;
(2)试探究:在AC上是否存在点F,满足EF//平面A1ABB1,若存在,请指出点F的位置,并给出证明;若不存在,说明理由.
(1)证明过程详见解析;(2)证明过程详见解析.
试题分析:本题主要以三棱柱为几何背景考查线线垂直,线面垂直、线面平行、面面平行等数学知识,考查学生的逻辑推理能力和空间想象能力,考查学生的数形结合思想.第一问,由于AA1⊥面ABC,所以利用线面垂直的性质得
 垂直面内的线BC,而
垂直面内的线BC,而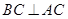 ,利用线面垂直的判定得
,利用线面垂直的判定得 面
面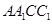 ,所以BC垂直于面
,所以BC垂直于面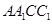 内的线
内的线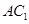 ;第二问,法一:先找到F点的位置,再证明,作出辅助线
;第二问,法一:先找到F点的位置,再证明,作出辅助线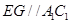 ,因为
,因为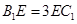 ,所以得到
,所以得到 ,而
,而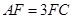 ,即
,即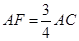 ,所以
,所以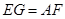 且
且 ,所以四边形AFEG为平行四边形,所以
,所以四边形AFEG为平行四边形,所以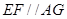 ,所以利用线面平行的判定得
,所以利用线面平行的判定得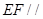 平面
平面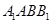 ;法二:作出辅助线
;法二:作出辅助线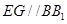 ,利用线面平行的判定,可以推断出
,利用线面平行的判定,可以推断出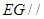 平面
平面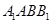 ,
,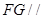 平面
平面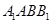 ,利用面面平行的判定,得面
,利用面面平行的判定,得面 平面
平面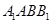 ,所以得
,所以得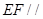 平面
平面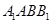 .
.试题解析:(1)∵AA1⊥面ABC,BC?面ABC,
∴BC⊥AA1.(1分)
又∵BC⊥AC,AA1,AC?面AA1C1C,AA1∩AC=A,∴BC⊥面AA1C1C,(3分)
又AC1?面AA1C1C,∴BC⊥AC1.(4分)
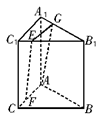
(2)(法一)当AF=3FC时,FE∥平面A1ABB1.(7分)
理由如下:在平面A1B1C1内过E作EG∥A1C1交A1B1于G,连结AG.
∵B1E=3EC1,∴
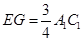 ,
,又AF∥A1C1且
 ,
,∴AF∥EG且AF=EG,
∴四边形AFEG为平行四边形,∴EF∥AG,(10分)
又EF?面A1ABB1,AG?面A1ABB1,∴EF∥平面A1ABB1.(12分)
(法二)当AF=3FC时,FE∥平面A1ABB1.(9分)
理由如下:在平面BCC1B1内过E作EG∥BB1交BC于G,连结FG.

∵EG∥BB1,EG?面A1ABB1,BB1?面A1ABB1,
∴EG∥平面A1ABB1.∵B1E=3EC1,∴BG=3GC,
∴FG∥AB,又AB?面A1ABB1,FG?面A1ABB1,
∴FG∥平面A1ABB1.
又EG?面EFG,FG?面EFG,EG∩FG=G,
∴平面EFG∥平面A1ABB1.(11分)
∵EF?面EFG,∴EF∥平面A1ABB1.(12分)

练习册系列答案
相关题目
 ABCD的底面是正方形,每条侧棱的长都是底面边长的
ABCD的底面是正方形,每条侧棱的长都是底面边长的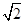 倍,P为侧棱SD上的点.
倍,P为侧棱SD上的点.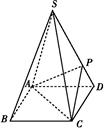
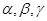 是三个不重合的平面,
是三个不重合的平面, 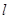 是直线,给出下列四个命题:①若
是直线,给出下列四个命题:①若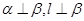 则
则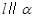 ;②若
;②若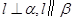 则
则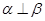 ;③若
;③若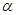 的距离相等,则
的距离相等,则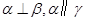 ,则
,则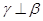 其中正确命题的序号 ( )
其中正确命题的序号 ( )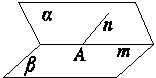
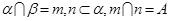
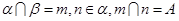
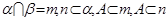
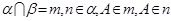
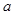 ,b,c是空间三条不同的直线,
,b,c是空间三条不同的直线,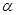 ,
,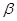 是空间两个不同的平面,则下列命题不成立的是( )
是空间两个不同的平面,则下列命题不成立的是( )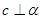 时,若
时,若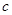 ⊥
⊥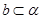 ,且
,且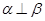
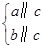 a∥b;②
a∥b;②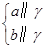 a∥b;③
a∥b;③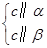 α∥β;
α∥β;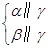 α∥β;⑤
α∥β;⑤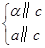 α∥a;⑥
α∥a;⑥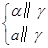 a∥α.
a∥α.