题目内容
设P是⊙O: 上的一点,以
上的一点,以 轴的非负半轴为始边、OP为终边的角记为
轴的非负半轴为始边、OP为终边的角记为 ,又向量
,又向量 。且
。且 .
.
(1)求 的单调减区间;
的单调减区间;
(2)若关于 的方程
的方程 在
在 内有两个不同的解,求
内有两个不同的解,求 的取值范围.
的取值范围.
【答案】
(1)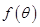 的单调减区间是:
的单调减区间是: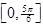 、
、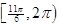 ;
;
(2)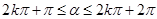 ,且
,且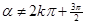
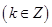 .
.
【解析】
试题分析:(1)由向量的数量积公式求出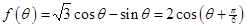 ,然后利用余弦函数的单调性即求得
,然后利用余弦函数的单调性即求得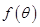 的单调减区间;(2)三角函数中的不等式或方程的问题都借助函数图象解决. 关于
的单调减区间;(2)三角函数中的不等式或方程的问题都借助函数图象解决. 关于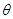 的方程
的方程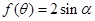 在
在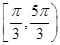 内有两个不同的解等价于直线
内有两个不同的解等价于直线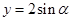 与函数
与函数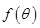 的图象在
的图象在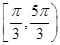 内有两个不同的交点.结合图象可找出
内有两个不同的交点.结合图象可找出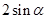 的范围,从而得
的范围,从而得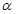 的范围.
的范围.
试题解析:(1)由条件知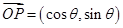 ,所以
,所以
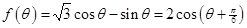
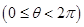 2分
2分
因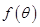 递减,则
递减,则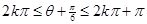 ,即
,即
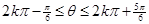
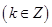 4分
4分
又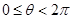 ,所以
,所以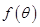 的单调减区间是:
的单调减区间是: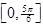 、
、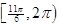 6分
6分
(2)因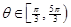 ,则
,则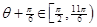 。为保证关于
。为保证关于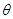 的方程
的方程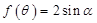 有两个不同解,借助函数图象可知:
有两个不同解,借助函数图象可知: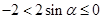 ,即
,即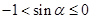 9分
9分
所以得: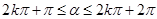 ,且
,且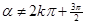
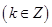 12分
12分
考点:

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 (2011•聊城一模)如图,四棱锥中S-ABCD中,底面ABCD是棱形,其对角线的交点为O,且SA=AC,SA⊥BD,
(2011•聊城一模)如图,四棱锥中S-ABCD中,底面ABCD是棱形,其对角线的交点为O,且SA=AC,SA⊥BD,