题目内容
4.已知函数f(x)=$\left\{\begin{array}{l}{{3}^{-x-1}-1(x≤-1)}\\{x+1(-1<x≤2)}\\{\sqrt{x-2}(x>2)}\end{array}\right.$,若f(a)>2,则a的取值范围是a>6或a<-2或1<a≤2.分析 讨论若a≤-1,若-1<a≤2,若a>2,由指数函数的性质和不等式的解法,即可得到a的范围.
解答 解:若a≤-1,f(a)>2即为3-a-1-1>2,解得-a-1>1,即a<-2,即为a<-2;
若-1<a≤2,f(a)>2即为a+1>2,即a>1,即有1<a≤2;
若a>2,f(a)>2即为$\sqrt{a-2}$>2,即a>6,即为a>6.
综上可得,a>6或a<-2或1<a≤2.
故答案为:a>6或a<-2或1<a≤2.
点评 本题考查分段函数的运用:解不等式,考查分类讨论的思想方法,以及运算能力,属于中档题.

练习册系列答案
相关题目
9.若函数f(x)的定义域是[0,4],则函数g(x)=$\frac{f(x+1)}{x}$的定义域是( )
| A. | [0,3] | B. | (-1,3) | C. | [-1,0)∪(0,3] | D. | (-1,3] |
13.已知数列{an}的通项公式为an=25-2n,在下列各数中,不是{an}的项的是( )
| A. | 1 | B. | -1 | C. | 3 | D. | 2 |
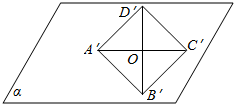 在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.
在水平放置的平面α内有一个边长为1的正方形A′B′C′D′.如图,其中的对角线A′C′在水平位置,已知该正方形是某个四边形用斜二测画法画出的直观图,试画出该四边形的真实图形并求出其面积.