题目内容
如图所示,已知PA切⊙O于A,割线PBC交⊙O于B、C,PD⊥AB于D,PD、AO的延长线相交于E,连结CE并延长交⊙O于F,连结AF.

(1)求证:△PBD∽△PEC;
(2)若AB=12,tan∠EAF=![]() ,求⊙O的半径.
,求⊙O的半径.
答案:
解析:
提示:
解析:
(1)证明:由切割定理,得PA2=PB·PC.
由△PAD∽△PEA,
得PA2=PD·PE.
所以PB·PC=PD·PE.
又∠BPD为公共角,
所以△PBD∽△PEC.
(2)解:作OG⊥AB于G,由△PBD∽△PEC,可得∠PEC=∠F,
因此PE∥AF.又OG⊥AB于G,所以AG=![]() AB=6.
AB=6.
所以OG∥ED∥FA.
所以∠AOG=∠EAF.
在Rt△AOG中,tan∠AOG=![]() ,
,
又![]() =
=![]() ,所以OG=9.
,所以OG=9.
由勾股定理,可得
AG2+OG2=AO2,
所以AO=![]() =3
=3![]() .
.
所以⊙O的半径长为3![]() .
.
分析:在(1)中,要证相似的两个三角形已经有一个角相等,只要再证其夹边对应成比例即可,而这可由△PAD∽△PEA得到;
在(2)中,已知tan∠EAF=![]() ,所以需构造直角三角形,从而利用三角函数求解.
,所以需构造直角三角形,从而利用三角函数求解.
提示:
已知条件中或图形中出现切线、割线等相关的条件时,通常需要借助于切割线定理建立线段之间的关系.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
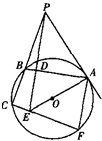 如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF. 于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
 时,求圆O的半径.
时,求圆O的半径.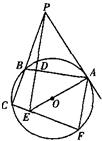
 时,求圆O的半径.
时,求圆O的半径.