题目内容
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.
(1)求证:B,C,E,D四点共圆;
(2)当AB=12,tan∠EAF=
时,求圆O的半径.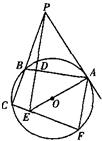
(1)求证:B,C,E,D四点共圆;
(2)当AB=12,tan∠EAF=
| 2 |
| 3 |

(1)由切割线定理PA2=PB?PC
由已知易得Rt△PAD∽Rt△PEA,∴PA2=PD?PE,
∴PA2=PB?PC=PA2=PD?PE,
又∠BPD为公共角,∴△PBD∽△PEC,
∴∠BDP=∠C
∴B,C,E,D四点共圆
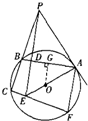
(2)作OG⊥AB于G,由(1)知∠PBD=∠PEC,
∵∠PBD=∠F,∴∠F=∠PEC,
∴PE∥AF.
∵AB=12,∴AG=6.
∵PD⊥AB,∴PD∥OG.
∴PE∥OG∥AF,
∴∠AOG=∠EAF.
在Rt△AOG中,tan∠AOG=tan∠EAF=
| 2 |
| 3 |
| 6 |
| OG |
∴OG=9∴R=AO=
| AG2+OG2 |
| 13 |
∴圆O的半径3
| 13 |

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
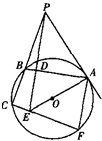 如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.
如图所示,已知PA切圆O于A,割线PBC交圆O于B、C,PD⊥AB于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF.
 于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
于D,PD与AO的延长线相交于点E,连接CE并延长交圆O于点F,连接AF。
 时,求圆O的半径.
时,求圆O的半径. 时,求圆O的半径.
时,求圆O的半径.