题目内容
已知函数f(x)=ax+k(a>0,a≠1)的图象过(-1,1)点,其反函数f-1(x)的图象过点(8,2).
1)求a、k的值(12’);
2)若将y=f-1(x)的图象向左平移2个单位,再向上平移1个单位,得到y=g(x)的图
像,写出y=g(x)的解析式;
3)若函数F(x)=g(x2)-f-1(x),求F(x)的最小值及取最小值时的x的值.
解:1)∵函数f(x)=ax+k(a>0,a≠1)的图象过(-1,1)点,
∴1=ak-1…①
又∵函数f(x)=ax+k其反函数f-1(x)的图象过点(8,2).
故函数f(x)=ax+k(a>0,a≠1)的图象过(2,8)点,
∴8=ak+2…①
由①②得
a=2,k=1
2)由1)得f(x)=2x+1
∴y=f-1(x)=log2x-1
将y=f-1(x)的图象向左平移2个单位,再向上平移1个单位,得到y=g(x)的图象,
∴y=g(x)=log2(x-2)-1+1
∴g(x)=log2(x+2),(x>-2);
3)∵函数F(x)=g(x2)-f-1(x),
又∵g(x)=log2(x+2),f-1(x)=log2x-1
∴g(x2)=log2(x2+2),
∴F(x)=g(x2)-f-1(x)=log2(x2+2)-log2x+1
∴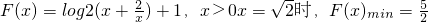 .
.
分析:1)由已知中函数f(x)=ax+k(a>0,a≠1)的反函数f-1(x)的图象过点(8,2),可得函数f(x)的图象过(2,8)点,再由函数f(x)的图象过(-1,1)点,代入构造关于a,k的方程组,解方程组即可得到a、k的值;
2)由1)中结论,我们可以求出函数f(x)的解析式,进而求出其反函数f-1(x)的解析式,再根据函数图象的平移变换法则,得到y=g(x)的解析式;
3)由函数F(x)=g(x2)-f-1(x),我们可以求出函数F(x)的解析式,根据基本不等式,我们可以确定出真数部分的取值范围,进而再由对数函数的单调性即可得到F(x)的最小值及取最小值时的x的值.
点评:本题考查的知识点是对数函数的图象与性质的综合应用,函数图象的平移变换,基本不等式在求函数最小值时的应用,反函数,其中(1)的关键是根据已知函数f(x)=ax+k的反函数f-1(x)的图象过点(8,2),得到函数f(x)的图象过(2,8)点,(2)的关键是熟练掌握函数图象的平移变换法则“左加右减,上加下减”,(3)的关键是利用基本不等式求出函数F(x)解析式中真数部分的最值.
∴1=ak-1…①
又∵函数f(x)=ax+k其反函数f-1(x)的图象过点(8,2).
故函数f(x)=ax+k(a>0,a≠1)的图象过(2,8)点,
∴8=ak+2…①
由①②得
a=2,k=1
2)由1)得f(x)=2x+1
∴y=f-1(x)=log2x-1
将y=f-1(x)的图象向左平移2个单位,再向上平移1个单位,得到y=g(x)的图象,
∴y=g(x)=log2(x-2)-1+1
∴g(x)=log2(x+2),(x>-2);
3)∵函数F(x)=g(x2)-f-1(x),
又∵g(x)=log2(x+2),f-1(x)=log2x-1
∴g(x2)=log2(x2+2),
∴F(x)=g(x2)-f-1(x)=log2(x2+2)-log2x+1
∴
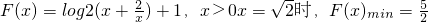 .
.分析:1)由已知中函数f(x)=ax+k(a>0,a≠1)的反函数f-1(x)的图象过点(8,2),可得函数f(x)的图象过(2,8)点,再由函数f(x)的图象过(-1,1)点,代入构造关于a,k的方程组,解方程组即可得到a、k的值;
2)由1)中结论,我们可以求出函数f(x)的解析式,进而求出其反函数f-1(x)的解析式,再根据函数图象的平移变换法则,得到y=g(x)的解析式;
3)由函数F(x)=g(x2)-f-1(x),我们可以求出函数F(x)的解析式,根据基本不等式,我们可以确定出真数部分的取值范围,进而再由对数函数的单调性即可得到F(x)的最小值及取最小值时的x的值.
点评:本题考查的知识点是对数函数的图象与性质的综合应用,函数图象的平移变换,基本不等式在求函数最小值时的应用,反函数,其中(1)的关键是根据已知函数f(x)=ax+k的反函数f-1(x)的图象过点(8,2),得到函数f(x)的图象过(2,8)点,(2)的关键是熟练掌握函数图象的平移变换法则“左加右减,上加下减”,(3)的关键是利用基本不等式求出函数F(x)解析式中真数部分的最值.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目