题目内容
14．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{x}，x≥2}\\{3-x，x＜2}\end{array}\right.$，则f（f（-1））的值为（ ）| A． | -1 | B． | 0 | C． | 1 | D． | 2 |
分析 利用分段函数的性质先求f（-1）的值，再求f（f（-1））的值．
解答 解：∵函数f（x）=$\left\{\begin{array}{l}{\sqrt{x}，x≥2}\\{3-x，x＜2}\end{array}\right.$，
∴f（-1）=3-（-1）=4，
f（f（-1））=f（4）=$\sqrt{4}$=2．
故选：D．
点评 本题考查函数值的求法，是基础题，解题时要认真审题，注意分段函数的性质的合理运用．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
6．已知$cosα=-\frac{3}{5}，α∈（0，π）$，则tanα=（ ）
| A． | $\frac{4}{3}$ | B． | $-\frac{4}{3}$ | C． | $±\frac{4}{3}$ | D． | $±\frac{3}{4}$ |
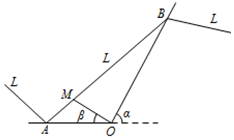如图，某城市有一条公路正西方AO通过市中心O后转向北偏东α角方向的OB，位于该市的某大学M与市中心O的距离OM=3$\sqrt{13}$km，且∠AOM=β，现要修筑一条铁路L，L在OA上设一站A，在OB上设一站B，铁路在AB部分为直线段，且经过大学M，其中tanα=2，cosβ=$\frac{3}{{\sqrt{13}}}$，AO=15km．