Question

（2012•德阳三模）将正方形ABCD沿对角线AC折起，当三棱锥B-ACD体积最大时，直线AD与BC所成角为（　　）

• A．

  π

  4

• B．

  π

  2

• C．

  π

  6

• D．

  π

  3

Answer 1

分析：将正方形ABCD沿对角线AC折起，可得当三棱锥B-ACD体积最大时，BO⊥平面ADC．设B'是B折叠前的位置，连接B'B，可得
∠BCB'就是直线AD与BC所成角，算出△BB'C的各边长，得△BB'C是等边三角形，从而得出直线AD与BC所成角的大小．

解答：解：设O是正方形对角线AC、BD的交点，将正方形ABCD沿对角线AC折起，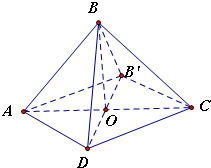
可得当BO⊥平面ADC时，点B到平面ACD的距离等于BO，
而当BO与平面ADC不垂直时，点B到平面ACD的距离为d，且d＜BO
由此可得当三棱锥B-ACD体积最大时，BO⊥平面ADC．
设B'是B折叠前的位置，连接B'B，
∵AD∥B'C，∴∠BCB'就是直线AD与BC所成角
设正方形ABCD的边长为a
∵BO⊥平面ADC，OB'?平面ACD
∴BO⊥OB'，
∵BO'=BO=

1

2

AC=

2

2

a，
∴BB'=BC=B'C=a，得△BB'C是等边三角形，∠BCB'=60°
所以直线AD与BC所成角为

π

3

，
故选D

点评：本题将正方形折叠，求所得锥体体积最大时异面直线所成的角，着重考查了线面垂直的性质和异面直线所成角求法等知识，属于中档题．