题目内容
已知函数
(I)当 时,求
时,求 在[1,
在[1, ]上的取值范围。
]上的取值范围。
(II)若 在[1,
在[1, ]上为增函数,求a的取值范围。
]上为增函数,求a的取值范围。
(1) 取值范围为[
取值范围为[ (2)
(2)
解析试题分析:解:(1) 时
时 

当 时
时 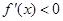
 在[1,2)上
在[1,2)上 时
时 
 在[2,
在[2, )上
)上
∴ 时
时  有极小值也就是最小值
有极小值也就是最小值
又
∴ 在[1,
在[1, ]上最大值为
]上最大值为
 取值范围为[
取值范围为[
(2)

设 要使
要使 在[1,
在[1, ]上 只须
]上 只须 
即 在[1,
在[1, ]上恒成立
]上恒成立 的对称轴为
的对称轴为 且开口向下
且开口向下
故只须
由此得出 取值范围为
取值范围为 
考点:导数的运用
点评:主要是考查了导数在研究函数单调性,以及极值和最值的运用,属于中档题。

练习册系列答案
相关题目
探究函数f(x)=x+ ,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 8.5 | 5 | 4.17 | 4.05 | 4.005 | 4 | 4.005 | 4.02 | 4.04 | 4.3 | 5 | 5.8 | 7.57 | … |
函数f(x)=x+
 (x>0)在区间(0,2)上递减;
(x>0)在区间(0,2)上递减;(1)函数f(x)=x+
 (x>0)在区间 上递增.
(x>0)在区间 上递增.当x= 时,y最小= .
(2)证明:函数f(x)=x+
 在区间(0,2)上递减.
在区间(0,2)上递减.(3)思考:函数f(x)=x+
 (x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)  有极值,
有极值, 的取值范围;
的取值范围; .
.  处取到极值?若有可能,求实数
处取到极值?若有可能,求实数 的值;否则说明理由;
的值;否则说明理由; 上为增函数,求实数
上为增函数,求实数 ,记
,记 的导函数
的导函数 ,
, 的导函数
的导函数 ,
,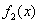 的导函数
的导函数 ,…,
,…, 的导函数
的导函数 ,
, .
. ;
; ;
; ,是否存在
,是否存在 使
使 最大?证明你的结论.
最大?证明你的结论. 和
和 是先后抛掷该枚骰子得到的数字,函数
是先后抛掷该枚骰子得到的数字,函数

 有零点的概率;
有零点的概率; 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式 对任意
对任意 恒成立.
恒成立. 的取值范围;
的取值范围; ,其中
,其中 ,
, .
. 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程; 的单调区间.(要写推理过程)
的单调区间.(要写推理过程) 满足:g(2)=4,定义域为
满足:g(2)=4,定义域为 的函数
的函数 是奇函数。
是奇函数。 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围