题目内容
已知抛物线y2=x,则过P(1,1)与抛物线有且只有一个交点的直线有( )条.
分析:易知符合条件的直线存在斜率,设直线方程为:y-1=k(x-1),与抛物线方程联立消掉y得x的方程,按照x2的系数为0,不为0两种情况进行讨论,其中不为0时令△=0可求.
解答: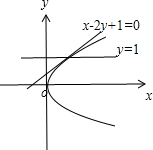 解:当直线不存在斜率时,不符合题意;
解:当直线不存在斜率时,不符合题意;
当直线存在斜率时,设直线方程为:y-1=k(x-1),
由
,k2x2+(2k-1-2k2)x+k2-2k+1=0,
当k=0时,方程为:-x+1=0,得x=1,此时只有一个交点(1,1),直线与抛物线相交;
当k≠0时,令△=(2k-1-2k2)2-4k2(k2-2k+1)=0,化简得,4k2-4k+1=0,
解得k=
,此时直线与抛物线相切,直线方程为:y-1=
(x-1),即x-2y+1=0;
综上,满足条件的直线有两条:方程为y=1,x-2y+1=0,如右图所示:
故选B.
 解:当直线不存在斜率时,不符合题意;
解:当直线不存在斜率时,不符合题意;当直线存在斜率时,设直线方程为:y-1=k(x-1),
由
|
当k=0时,方程为:-x+1=0,得x=1,此时只有一个交点(1,1),直线与抛物线相交;
当k≠0时,令△=(2k-1-2k2)2-4k2(k2-2k+1)=0,化简得,4k2-4k+1=0,
解得k=
| 1 |
| 2 |
| 1 |
| 2 |
综上,满足条件的直线有两条:方程为y=1,x-2y+1=0,如右图所示:
故选B.
点评:本题考查直线与抛物线的位置关系,考查分类讨论思想,考查学生分析解决问题的能力,属中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 (2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….
(2012•西城区一模)如图,已知抛物线y2=x及两点A1(0,y1)和A2(0,y2),其中y1>y2>0.过A1,A2分别作y轴的垂线,交抛物线于B1,B2两点,直线B1B2与y轴交于点A3(0,y3),此时就称A1,A2确定了A3.依此类推,可由A2,A3确定A4,….记An(0,yn),n=1,2,3,….