题目内容
已知数列{an}为等差数列,a1=2,且其前10项和为65,又正项数列{bn}满足bn=| n+1 | an |
(1)求数列{bn}的通项公式;
(2)比较b1,b2,b3,b4的大小;
(3)求数列{bn}的最大项.
分析:(1)设{an}的公差为d,则65=10a1+
d,再由a1=2,得d=1,由此能够求出数列{bn}的通项公式.
(2)b1=
=
<
=
=b2,b3=
=
=b1,b3=
=
>
=
=b4,由此能够判断b1,b2,b3,b4的大小.
(3)猜想当n≥2时,
>
.函数y=
(x>e)中,y′=
<0,故y=
在(e,+∞)上是减函数,所以
<
.猜想正确,因此,数列{bn}的最大项是b2=
.
| 10×9 |
| 2 |
(2)b1=
| 2 |
| 6 | 23 |
| 6 | 32 |
| 3 | 3 |
| 4 | 4 |
| 2 |
| 4 | 4 |
| 20 | 45 |
| 20 | 54 |
| 5 | 5 |
(3)猜想当n≥2时,
| n+1 | n+1 |
| n+2 | n+2 |
| lnx |
| x |
| 1-lnx |
| x2 |
| lnx |
| x |
| n+2 | n+2 |
| n+1 | n+1 |
| 3 | 3 |
解答:解:(1)设{an}的公差为d,则65=10a1+
d,又a1=2,得d=1,从而an=n+1
故bn=
.(4分)
(2)b1=
=
<
=
=b2,
b3=
=
=b1,
b3=
=
>
=
=b4,
∴b2>b1=b3>b4.(8分)
(3)由(2)猜想{bn+1}递减,即猜想当n≥2时,
>
.(10分)
考察函数y=
(x>e),
则y′=
,∵x>e时,lnx>1,∴y'<0,
故y=
在(e,+∞)上是减函数,而n+1≥3>e,(12分)
所以
<
,即
<
.
猜想正确,因此,数列{bn}的最大项是b2=
.(14分)
| 10×9 |
| 2 |
故bn=
| n+1 | n+1 |
(2)b1=
| 2 |
| 6 | 23 |
| 6 | 32 |
| 3 | 3 |
b3=
| 4 | 4 |
| 2 |
b3=
| 4 | 4 |
| 20 | 45 |
| 20 | 54 |
| 5 | 5 |
∴b2>b1=b3>b4.(8分)
(3)由(2)猜想{bn+1}递减,即猜想当n≥2时,
| n+1 | n+1 |
| n+2 | n+2 |
考察函数y=
| lnx |
| x |
则y′=
| 1-lnx |
| x2 |
故y=
| lnx |
| x |
所以
| ln(n+2) |
| n+2 |
| ln(n+1) |
| n+1 |
| n+2 | n+2 |
| n+1 | n+1 |
猜想正确,因此,数列{bn}的最大项是b2=
| 3 | 3 |
点评:自从导数走进高考试题中,就和函数形影不离,并且与方程、数列、解析几何以及立体几何等分支的知识联姻,成为高考的一道亮丽的风景线.预计导数还会与平面向量、概率与统计等分支的知识联合,展示其独特的魅力.

练习册系列答案
相关题目
定义:在数列{an}中,an>0且an≠1,若
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009=( )
| a | an+1 n |
| A、6026 | B、6024 |
| C、2 | D、4 |

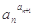 为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4
为定值,则称数列{an}为“等幂数列”.已知数列{an}为“等幂数列”,且a1=2,a2=4,Sn为数列{an}的前n项和,则S2009= ( )A.6026
B .6024 C.2
D.4