题目内容
19.将函数y=f(x)的图象向左平移1个单位长度,纵坐标不变,横坐标缩小到原来的$\frac{3}{π}$倍,然后再向上平移1个单位长度,得到函数y=$\sqrt{3}$sinx的图象.(1)求f(x)的最小正周期和单调递增区间;
(2)求使得y=f(x)取得最值的自变量的集合.
分析 (1)由条件利用函数y=Asin(ωx+φ)的图象变换规律,可得f(x)的解析式,再根据正弦函数的周期性、单调性求得f(x)的最小正周期和单调递增区间.
(2)根据函数的解析式、正弦函数的定义域和值域,求出使得y=f(x)取得最值的自变量的集合.
解答 解:(1)由题意可得把函数y=$\sqrt{3}$sinx的图象向下平移1个单位长度,可得y=$\sqrt{3}$sinx-1的图象;
再把所得图象的纵坐标不变,横坐标变为原来的$\frac{π}{3}$倍,可得f(x)=$\sqrt{3}$sin($\frac{π}{3}$x)-1的图象;
再把所得图象向右平移1个单位长度,可得y=$\sqrt{3}$sin$\frac{π}{3}$(x-1)-1=$\sqrt{3}$sin($\frac{π}{3}$x-$\frac{π}{3}$)-1 的图象;
故f(x)的最小正周期为$\frac{2π}{\frac{π}{3}}$=6.
令2kπ-$\frac{π}{2}$≤$\frac{π}{3}$x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈z,求得6k-$\frac{1}{2}$≤x≤6k+$\frac{5}{2}$,
故函数的增区间为[6k-$\frac{1}{2}$,6k+$\frac{5}{2}$],k∈z.
(2)对于f(x)=$\sqrt{3}$sin($\frac{π}{3}$x-$\frac{π}{3}$)-1,当$\frac{π}{3}$x-$\frac{π}{3}$=kπ+$\frac{π}{2}$,即x=3k+$\frac{5}{2}$,k∈z时,函数f(x)取得最值.
故使得y=f(x)取得最值的自变量的集合为{x|x=3k+$\frac{5}{2}$,k∈z}.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的周期性、单调性、定义域和值域,属于中档题.

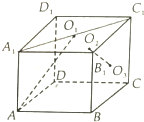 已知O1,O2,O3分别是正方体ABCD-A1B1C1D1的三个面A1B1C1D1,CC1D1D,BCC1B1的中点,求异面直线AO1与O2O3所成角的大小.
已知O1,O2,O3分别是正方体ABCD-A1B1C1D1的三个面A1B1C1D1,CC1D1D,BCC1B1的中点,求异面直线AO1与O2O3所成角的大小. 如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC=$\frac{2}{3}$AB,又PO⊥平面ABC,DA∥PO,DA=AO=$\frac{1}{2}$PO.
如图,在△ABC中,已知∠ABC=45°,O在AB上,且OB=OC=$\frac{2}{3}$AB,又PO⊥平面ABC,DA∥PO,DA=AO=$\frac{1}{2}$PO.