��Ŀ����
7����֪����f��x��=lnx��g��x��=ax2-bx��a��0��������b=0ʱ������h��x��=f��x��-g��x���ĵ������䣻
����b=1ʱ���ش������������⣺
��i��������y=f��x���뺯��y=g��x����ͼ���ڹ�����P������ͬ�����ߣ���ʵ��a��ֵ��
��ii��������y=f��x���뺯��y=g��x����ͼ����������ͬ�Ľ���M��N�����߶�MN���е���x��Ĵ��ߣ��ֱ���f��x����g��x����ͼ����S��T���㣮��SΪ�е���f��x������l1����TΪ�е���g��x��������l2���Ƿ����ʵ��a��ʹ��l1��l2�������ڣ����a��ֵ���������ڣ���˵�����ɣ�
���� ���������⣬h��x��=f��x��-g��x��=lnx-ax2��x��0�����ɵ�h�䣨x��=$\frac{1}{x}$-2ax=$\frac{1-2a{x}^{2}}{x}$���Ӷ��ɵ���������ȷ���䵥���Լ��������䣻
����i���躯��y=f��x���뺯��y=g��x����ͼ��Ĺ�����P��x0��y0��������lnx0=ax02-x0��f�䣨x0��=g�䣨x0�����Ӷ��ɵ�lnx0=$\frac{1}{2}$-$\frac{1}{2}$x0������H��x��=lnx-$\frac{1}{2}$+$\frac{1}{2}$x��H�䣨x��=$\frac{1}{x}$+$\frac{1}{2}$��0���Ӷ���a��
��ii��������M��x1��y1����N��x2��y2����x1��x2����MN�е������Ϊ��$\frac{{x}_{1}+{x}_{2}}{2}$��$\frac{{y}_{1}+{y}_{2}}{2}$�����Ӷ�д�����ߵ�б��k1=f�䣨$\frac{{x}_{1}+{x}_{2}}{2}$��=$\frac{2}{{x}_{1}+{x}_{2}}$��k2=g�䣨$\frac{{x}_{1}+{x}_{2}}{2}$��=a��x1+x2��-1���Ӷ��������aʹ��k1=k2��$\frac{2}{{x}_{1}+{x}_{2}}$=a��x1+x2��-1���ٽ��lnx1=ax12-x1��lnx2=ax22-x2��ln$\frac{{x}_{1}}{{x}_{2}}$=$\frac{2��\frac{{x}_{1}}{{x}_{2}}-1��}{\frac{{x}_{1}}{{x}_{2}}+1}$����u=$\frac{{x}_{1}}{{x}_{2}}$��1������lnu=$\frac{2��u-1��}{u+1}$����u��1�����Ӷ���ȷ������������ʵ��a�������ڣ�
��� �⣺���������⣬h��x��=f��x��-g��x��=lnx-ax2��x��0����
���ԣ�h�䣨x��=$\frac{1}{x}$-2ax=$\frac{1-2a{x}^{2}}{x}$��
���ԣ���a��0ʱ��h�䣨x����0��h��x������������
��a��0ʱ��f��x���ĵ���������Ϊ��0��$\sqrt{\frac{1}{2a}}$��������������Ϊ��$\sqrt{\frac{1}{2a}}$��+�ޣ���
����i���躯��y=f��x���뺯��y=g��x����ͼ��Ĺ�����P��x0��y0��������
lnx0=ax02-x0����
���ڵ�P�й�ͬ�����ߣ�
��f�䣨x0��=g�䣨x0����
��$\frac{1}{{x}_{0}}$=2ax0-1��
��a=$\frac{1+{x}_{0}}{2{x}_{0}^{2}}$����ٵ�
lnx0=$\frac{1}{2}$-$\frac{1}{2}$x0��
��H��x��=lnx-$\frac{1}{2}$+$\frac{1}{2}$x��H�䣨x��=$\frac{1}{x}$+$\frac{1}{2}$��0��
���Ժ���H��x�����ֻ��1����㣬�۲��x0=1����㣮
��a=1����ʱP��1��0����
��ii��������M��x1��y1����N��x2��y2����x1��x2����MN�е������Ϊ��$\frac{{x}_{1}+{x}_{2}}{2}$��$\frac{{y}_{1}+{y}_{2}}{2}$����
��SΪ�е������l1��б��k1=f�䣨$\frac{{x}_{1}+{x}_{2}}{2}$��=$\frac{2}{{x}_{1}+{x}_{2}}$��
��TΪ�е������l2��б��k2=g�䣨$\frac{{x}_{1}+{x}_{2}}{2}$��=a��x1+x2��-1��
�������aʹ��k1=k2��$\frac{2}{{x}_{1}+{x}_{2}}$=a��x1+x2��-1����
������lnx1=ax12-x1��lnx2=ax22-x2��
������ٵ����߳�x1-x2�ò���ɵã�
$\frac{2��{x}_{1}-{x}_{2}��}{{x}_{1}+{x}_{2}}$=ax12-x1-��ax22-x2��=lnx1-lnx2=ln$\frac{{x}_{1}}{{x}_{2}}$��
����ln$\frac{{x}_{1}}{{x}_{2}}$=$\frac{2��\frac{{x}_{1}}{{x}_{2}}-1��}{\frac{{x}_{1}}{{x}_{2}}+1}$��
��u=$\frac{{x}_{1}}{{x}_{2}}$��1������lnu=$\frac{2��u-1��}{u+1}$����u��1����
����F��u��=lnu-$\frac{2��u-1��}{u+1}$����u��1���ĵ����Բ��ѷ��֣�
F��u����[1��+�ޣ��ϵ�����������F��u����F��1��=0��
���ԣ�����������ʵ��a�������ڣ�
���� ���⿼���˵������ۺ�Ӧ�ü��������������Ӧ�ã�������������ѣ��������⣮


| A�� | 4 | B�� | 21+$\sqrt{3}$ | C�� | 3$\sqrt{3}$+12 | D�� | $\frac{{3\sqrt{3}}}{2}$+12 |
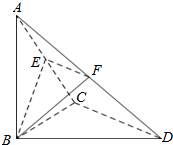 ��ͼ5����֪��BCD�У���BCD=90�㣬BC=CD=1��AB=$\sqrt{6}$��AB��ƽ��BCD��E��F�ֱ���AC��AD���е㣮
��ͼ5����֪��BCD�У���BCD=90�㣬BC=CD=1��AB=$\sqrt{6}$��AB��ƽ��BCD��E��F�ֱ���AC��AD���е㣮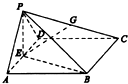 ��ͼ��������P-ABCD�У�����ABCD�������Σ�ƽ��PAD��ƽ��ABCD��PA=PD=$\sqrt{2}$����PA��PD��E���߶�AD���е㣮
��ͼ��������P-ABCD�У�����ABCD�������Σ�ƽ��PAD��ƽ��ABCD��PA=PD=$\sqrt{2}$����PA��PD��E���߶�AD���е㣮 ��ͼ�������� ADEF ������ ABCD����ƽ�滥�ഹֱ����֪ AB��CD��AD��CD��AB=AD=$\frac{1}{2}$CD��
��ͼ�������� ADEF ������ ABCD����ƽ�滥�ഹֱ����֪ AB��CD��AD��CD��AB=AD=$\frac{1}{2}$CD��