题目内容
已知函数f(x)=x3-ax,
(Ⅰ)当a=3时,求f(x)在[-2,2]上的最大值和最小值;
(Ⅱ)已知函数g(x)=ax(|x+a|-1),记h(x)=f(x)-g(x)(x∈[0,2]),当函数h(x)的最大值为0时,求实数a的取值范围。
(Ⅰ)当a=3时,求f(x)在[-2,2]上的最大值和最小值;
(Ⅱ)已知函数g(x)=ax(|x+a|-1),记h(x)=f(x)-g(x)(x∈[0,2]),当函数h(x)的最大值为0时,求实数a的取值范围。
解:(Ⅰ)∵f(x)=x3-3x,
∴f′(x)=3x2-3=3(x-1)(x+1),
∵f′(x)>0 x>1或x<-1,且x∈[-2,2],
x>1或x<-1,且x∈[-2,2],
∴函数f(x)在[-2,-1]上递增,[-1,1]上递减,[1,2]上递增,
∵f(-2)=f(1)=-2,
∴fmin(x)=-2,
∵f(0)=-2,而f(2)=2,
∴fmax(x)=2;
(Ⅱ)h(x)=f(x)-g(x)=x3-ax|x+a|(x∈[0,2]),
(1)当a≤0时,h(x)=x3-ax|x+a|≥0,
∵h(0)=0,且0<x≤2时h(x)>0,显然不符合题设;
(2)当a>0时,∵x≥0,h(x)=x3-ax2-a2x,
∴h′(x)=3x2-2ax-a2=(x-a)(3x+a),
∵x≥0,
∴h′(x)>0 x>a,
x>a,
①当a≥2时,必有h′(x)≤0,
∴h(x)在[0,2]上单调递减,则最大值为h(0)=0,满足题设;
②当0<a<2时,∵h′(x)>0 x>a,
x>a,
∴h(x)在[0,a]上单调递减,(a,2]上单调递增,
则h(x)max=max(h(0),h(2)),
∵h(0)=0,只需h(2)≤0,即8-4a-2a2≤0,
解得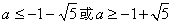 ,
,
∴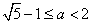 ;
;
综上得,所求实数a的取值范围是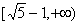 。
。
∴f′(x)=3x2-3=3(x-1)(x+1),
∵f′(x)>0
 x>1或x<-1,且x∈[-2,2],
x>1或x<-1,且x∈[-2,2],∴函数f(x)在[-2,-1]上递增,[-1,1]上递减,[1,2]上递增,
∵f(-2)=f(1)=-2,
∴fmin(x)=-2,
∵f(0)=-2,而f(2)=2,
∴fmax(x)=2;
(Ⅱ)h(x)=f(x)-g(x)=x3-ax|x+a|(x∈[0,2]),
(1)当a≤0时,h(x)=x3-ax|x+a|≥0,
∵h(0)=0,且0<x≤2时h(x)>0,显然不符合题设;
(2)当a>0时,∵x≥0,h(x)=x3-ax2-a2x,
∴h′(x)=3x2-2ax-a2=(x-a)(3x+a),
∵x≥0,
∴h′(x)>0
 x>a,
x>a,①当a≥2时,必有h′(x)≤0,
∴h(x)在[0,2]上单调递减,则最大值为h(0)=0,满足题设;
②当0<a<2时,∵h′(x)>0
 x>a,
x>a,∴h(x)在[0,a]上单调递减,(a,2]上单调递增,
则h(x)max=max(h(0),h(2)),
∵h(0)=0,只需h(2)≤0,即8-4a-2a2≤0,
解得
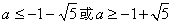 ,
,∴
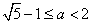 ;
;综上得,所求实数a的取值范围是
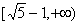 。
。 
练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|