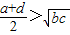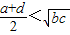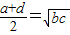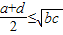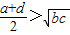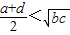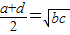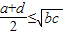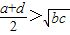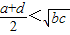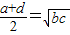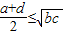题目内容
四个不相等的正数a、b、c、d成等差数列，则下列关系式一定成立的是
- A.
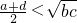
- B.
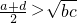
- C.
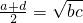
- D.
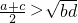
B
分析：根据等差数列的定义和性质可得b+c=a+d，再由基本不等式可得b+c＞
，从而得到答案．
解答：由于四个不相等的正数a、b、c、d成等差数列，故 b+c=a+d，又由基本不等式可得b+c＞，
故选B．
点评：本题考查等差数列的定义和性质，基本不等式的应用，得到b+c=a+d，是解题的关键．
分析：根据等差数列的定义和性质可得b+c=a+d，再由基本不等式可得b+c＞
，从而得到答案．解答：由于四个不相等的正数a、b、c、d成等差数列，故 b+c=a+d，又由基本不等式可得b+c＞
，故选B．
点评：本题考查等差数列的定义和性质，基本不等式的应用，得到b+c=a+d，是解题的关键．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
四个不相等的正数a、b、c、d成等差数列，则下列关系式一定成立的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
