题目内容
9．
如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于点D，DE⊥AC，交AC的延长线于点E．若AE=8，AB=10，则CE的长为2．
分析 连接CD，BD，根据角平分线定义以及圆周角定理得到△DCE≌△DBH，设CE=a，CD=x，结合勾股定理列出方程解之．
解答 解：连接CD，BD，过D作DH⊥AB，垂足为H，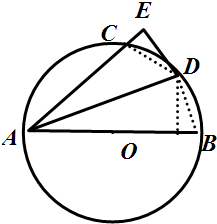
因为∠BAC的平分线AD交⊙O于点D，所以CD=BD，
则△DCE≌△DBH，
所以CE=BH=a，
设CE=a，CD=x，
在直角三角形ABD中，DH2=AH×BH，并且AD2=AE2-DE2=AB2-BD2，
即x2-a2=（10-a）a，①
64+x2-a2=100-x2，②
由①②得a=2．即CE=2；
故答案为：2．
点评 本题考查了圆周角定理、方程思想求线段的长度．
练习册系列答案
相关题目
如图，P是平面ABCD外的一点，PA⊥平面ABCD，四边形ABCD是边长为2的正方形，PA=2，M、N分别为AD、BC的中点，MQ⊥PD于Q点．
如图，在正方体ABCD-A1B1C1D1中，点E是AB的中点，点F是AD的中点，求证：平面AA1C1C⊥平面A1EF．