Question

20．函数f（x）=|x²-4x+3|的单调增区间为[1，2]，[3，+∞），单调减区间为（-∞，1]，[2，3]．

Answer 1

分析 根据二次函数的图象和性质，及函数图象的对折变换法则，画出函数f（x）=|x²-4x+3|的图象，数形结合，可得答案．

解答 解：函数f（x）=|x²-4x+3|的图象由函数y=x²-4x+3的图象作一次纵向对折变换得到：
如下图所示：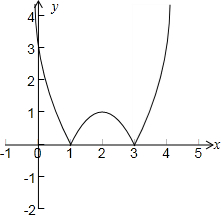

由图可得：函数f（x）=|x²-4x+3|的单调增区间为[1，2]，[3，+∞），
单调减区间为（-∞，1]，[2，3]，
故答案为：[1，2]，[3，+∞）；（-∞，1]，[2，3]

点评 本题考查的知识点是二次函数的图象和性质，及函数图象的对折变换法则，难度中档．