题目内容
5.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1(a>b>0)$的右焦点为F,上顶点为B,若线段BF的垂直平分线经过坐标原点O.(Ⅰ)求此椭圆的离心率;
(Ⅱ)过坐标原点引两条相互垂直的直线OM,ON(与坐标轴不重合)分别交椭圆于M,N两点,若三角形OMN的最小面积为$\sqrt{2}$,求椭圆方程.
分析 (Ⅰ)根据线段BF的垂直平分线经过坐标原点O得到b=c,即可求此椭圆的离心率;
(Ⅱ)设出直线OM,ON的方程,联立方程组求出M,N的横坐标,表示出三角形的面积,利用基本不等式进行求解即可.
解答 解:(Ⅰ)设F(c,0),B(0,b),
∵线段BF的垂直平分线经过坐标原点O,
∴b=c,
则a=$\sqrt{{b}^{2}+{c}^{2}}=\sqrt{2}c$,
即椭圆的离心率e=$\frac{c}{a}=\frac{\sqrt{2}}{2}$;
(Ⅱ)设直线OM的方程为y=kx,则直线ON的方程为y=-$\frac{1}{k}x$,
由$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{2{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,解得,${{x}_{M}}^{2}=\frac{2{b}^{2}}{1+2{k}^{2}}$,${{x}_{N}}^{2}$=$\frac{2{b}^{2}{k}^{2}}{2+{k}^{2}}$,
则S△OMN=$\frac{1}{2}•\sqrt{1+{k}^{2}}$•|xM|$•\sqrt{1+(-\frac{1}{k})^{2}}•|{x}_{N}|$=$\frac{1}{2}\sqrt{\frac{(1+{k}^{2})^{2}}{{k}^{2}}}$•|xM•xN|
=${b}^{2}•\sqrt{\frac{1}{2}-\frac{1}{4({k}^{2}+\frac{1}{{k}^{2}})+10}}$≥b2$•\sqrt{\frac{1}{2}-\frac{1}{4•2\sqrt{{k}^{2}•\frac{1}{{k}^{2}}}+10}}$=$\frac{2}{3}{b}^{2}$,
当且仅当k2=1时,取等号,即b2=3,
∴椭圆的方程为$\frac{{x}^{2}}{6}+\frac{{y}^{2}}{3}=1$.
点评 本题主要考查椭圆方程的求解以及椭圆离心率的求解,考查学是的运算能力.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案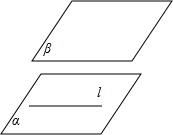
| A. | α∩β=l | B. | α∥β,l∈α | C. | l∥β,l?α | D. | α∥β,l?α |
 如图,在正三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E分别是CC1,AB的中点.
如图,在正三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,D,E分别是CC1,AB的中点.