题目内容
设数列
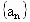 的前n项和为
的前n项和为 ,且
,且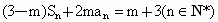 ,其中m为常数,且m≠-3.
,其中m为常数,且m≠-3.
(1)
求证: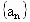 是等比数列;(2)若数列
是等比数列;(2)若数列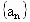 的公比q=f(m),数列
的公比q=f(m),数列 满足
满足 ,
, ,求证:
,求证: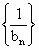 为等差数列.
为等差数列.
答案:略
解析:
提示:
解析:
|
(1)由 (2) 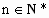 ,n≥2时, ,n≥2时,
∴  是首项为1,公差为 是首项为1,公差为 的等差数列. 的等差数列.
|
提示:
|
解析:本题要证明数列为等差、等比数列,通过定义可寻求解题思路,在证明过程中,恰当处理递推关系是本题证明的关键. |

练习册系列答案
相关题目
 得,
得,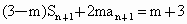 .两式相减得
.两式相减得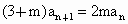 ,(m≠-3),∴
,(m≠-3),∴
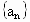 是等比数列.
是等比数列.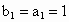
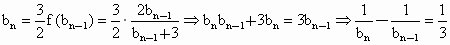
 的前n项和为Sn=2n2,
的前n项和为Sn=2n2,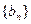 为等比数列,且
为等比数列,且 (Ⅰ)求数列
(Ⅰ)求数列 ,求数列
,求数列 的前n项和Tn.
的前n项和Tn.