题目内容
分析与综合法证明不等式:已知a+b+c=0,求证:ab+bc+ca≤0.
分析:先把a+b+c=0两边分别平方,得:(a+b+c)2=0,然后展开移向得:ab+bc+ca=-
,即可得到答案.
| a2+b2+c2 |
| 2 |
解答:解:证明:因为a+b+c=0,所以(a+b+c)2=0.
展开得ab+bc+ca=-
≤0,
所以ab+bc+ca≤0.
展开得ab+bc+ca=-
| a2+b2+c2 |
| 2 |
所以ab+bc+ca≤0.
点评:此题主要考查综合法证明不等式,有一定的灵活性,属于中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
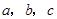 是不全相等的实数,求证:
是不全相等的实数,求证: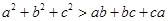 .
.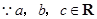 ,
,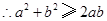 ,
,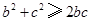 ,
,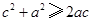 ,
,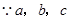 不全相等,
不全相等,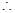 以上三式至少有一个“
以上三式至少有一个“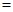 ”不成立,
”不成立,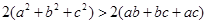 ,
,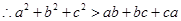 .
.