题目内容
(1)用综合法证明:a2+b2+c2≥ab+bc+ca,(a,b,c∈R+);
(2)用分析法证明:若a,b,m∈R+,且b<a,则
<
.
(2)用分析法证明:若a,b,m∈R+,且b<a,则
| b |
| a |
| b+m |
| a+m |
分析:(1)由于已知 a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac,相加后两边同时除以2,即得所证.
(2)寻找使
<
成立的充分条件,直到使不等式成立的条件显然具备为止.
(2)寻找使
| b |
| a |
| b+m |
| a+m |
解答:(1)证明:∵a2+b2≥2ab,b2+c2≥2bc,a2+c2≥2ac,
相加可得 2(a2+b2+c2)≥2(ab+bc+ca),
∴a2+b2+c2≥ab+bc+ca,(当且仅当a=b=c时,取等号).
(2)证明:∵a,b,m∈R+,且b<a,要证
<
,只要证 b(a+m)<a(b+m),
只要证bm<am,即证 b<a.
而b<a为已知条件,故要证的不等式成立.
相加可得 2(a2+b2+c2)≥2(ab+bc+ca),
∴a2+b2+c2≥ab+bc+ca,(当且仅当a=b=c时,取等号).
(2)证明:∵a,b,m∈R+,且b<a,要证
| b |
| a |
| b+m |
| a+m |
只要证bm<am,即证 b<a.
而b<a为已知条件,故要证的不等式成立.
点评:本题主要考查用综合法和分析法证明不等式,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
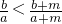 .
.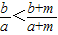 .
.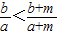 .
.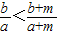 .
.