题目内容
定义在[1,4]上的函数f(x)=x2-2bx+
(1)b=1时,求函数的最值;
(2)若函数是单调函数,求b的取值范围.
【答案】分析:(1)将b=1代入可求出函数f(x)的解析式,进而根据二次函数的图象和性质,分析出函数在区间[1,4]上的单调性,进而得到最值.
(2)若函数是单调函数,则区间[1,4]在对称轴x=b的同一侧,由此可得b的取值范围.
解答:解:(1).当b=1时,f(x)=x2-2x+ ,…(2分)
,…(2分)
则函数f(x)在区间[1,4]单调递增,
所以f(1)=- 是最小值…(4分)
是最小值…(4分)
f(4)=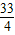 是最大值….(6分)
是最大值….(6分)
(2)对称轴x=b,若函数是单调函数,…(8分)
…则b≥4或b≤1
故b的取值范围(-∞,1]∪[4,+∞)
点评:本题考查的知识点是二次函数在闭区间上的最值,函数的单调性的判断与证明,熟练掌握二次函数的图象和性质是解答的关键.
(2)若函数是单调函数,则区间[1,4]在对称轴x=b的同一侧,由此可得b的取值范围.
解答:解:(1).当b=1时,f(x)=x2-2x+
 ,…(2分)
,…(2分)则函数f(x)在区间[1,4]单调递增,
所以f(1)=-
 是最小值…(4分)
是最小值…(4分)f(4)=
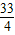 是最大值….(6分)
是最大值….(6分)(2)对称轴x=b,若函数是单调函数,…(8分)
…则b≥4或b≤1
故b的取值范围(-∞,1]∪[4,+∞)
点评:本题考查的知识点是二次函数在闭区间上的最值,函数的单调性的判断与证明,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目