题目内容
已知定义在[1,4]上的函数f(x)=x2-2bx+
(b≥1),
( I)求f(x)的最小值g(b);
( II)求g(b)的最大值M.
| b | 4 |
( I)求f(x)的最小值g(b);
( II)求g(b)的最大值M.
分析:(I)由已知中函数的解析式,可得f(x)=(x-b)2-b2+
的对称轴为直线x=b(b≥1),分当1≤b≤4时,和b>4时,两种情况,分析函数在区间[1,4]上的单调性,可得f(x)的最小值g(b);
( II)结合(I)中所得g(b)的解析式,根据分段函数分段处理的原则,分别求出各段上函数的最大值,比照后可得g(b)的最大值M.
| b |
| 4 |
( II)结合(I)中所得g(b)的解析式,根据分段函数分段处理的原则,分别求出各段上函数的最大值,比照后可得g(b)的最大值M.
解答:解:f(x)=(x-b)2-b2+
的对称轴为直线x=b(b≥1),
( I)①当1≤b≤4时,g(b)=f(b)=-b2+
;
②当b>4时,g(b)=f(4)=16-
b,
综上所述,f(x)的最小值g(b)=
.
( II)①当1≤b≤4时,g(b)=-b2+
=-(b-
)2+
,
∴当b=1时,M=g(1)=-
;
②当b>4时,g(b)=16-
b是减函数,∴g(b)<16-
×4=-15<-
,
综上所述,g(b)的最大值M=-
.
| b |
| 4 |
( I)①当1≤b≤4时,g(b)=f(b)=-b2+
| b |
| 4 |
②当b>4时,g(b)=f(4)=16-
| 31 |
| 4 |
综上所述,f(x)的最小值g(b)=
|
( II)①当1≤b≤4时,g(b)=-b2+
| b |
| 4 |
| 1 |
| 8 |
| 1 |
| 64 |
∴当b=1时,M=g(1)=-
| 3 |
| 4 |
②当b>4时,g(b)=16-
| 31 |
| 4 |
| 31 |
| 4 |
| 3 |
| 4 |
综上所述,g(b)的最大值M=-
| 3 |
| 4 |
点评:本题考查的知识点是二次函数在闭区间上的最值,函数单调性的性质,其中熟练掌握二次函数的图象和性质,是解答本题的关键.

练习册系列答案
相关题目
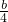 (b≥1),
(b≥1), (b≥1),
(b≥1), (b≥1),
(b≥1),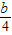 (b≥1),
(b≥1),