题目内容
已知椭圆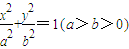 的右焦点为F(c,0),过F作与x轴垂直的直线与椭圆相交于点P,过点P的椭圆的切线l与x轴相交于点A,则点A的坐标为 .
的右焦点为F(c,0),过F作与x轴垂直的直线与椭圆相交于点P,过点P的椭圆的切线l与x轴相交于点A,则点A的坐标为 .
【答案】分析:先设P(c,y)(y>0),利用椭圆的方程求出点P的坐标(c,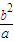 ),利用过椭圆上一点P(m,n)的切线方程为
),利用过椭圆上一点P(m,n)的切线方程为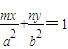 ,求出切线的方程,即可得出A点的坐标.
,求出切线的方程,即可得出A点的坐标.
解答: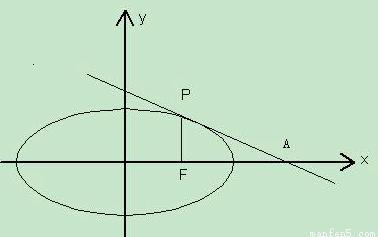 解:如图,设P(c,y)(y>0),则
解:如图,设P(c,y)(y>0),则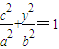 ,
,
∴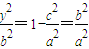 ,
,
∴y=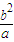 ,
,
∴P(c,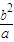 ),
),
∴过点P的切线方程为: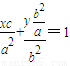 ,
,
令y=0,得x=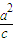 ,
,
∴A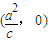 .
.
故答案为: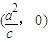 .
.
点评:本小题主要考查椭圆的简单性质、椭圆的切线等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.
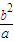 ),利用过椭圆上一点P(m,n)的切线方程为
),利用过椭圆上一点P(m,n)的切线方程为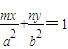 ,求出切线的方程,即可得出A点的坐标.
,求出切线的方程,即可得出A点的坐标.解答:
 解:如图,设P(c,y)(y>0),则
解:如图,设P(c,y)(y>0),则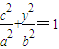 ,
,∴
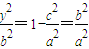 ,
,∴y=
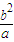 ,
,∴P(c,
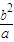 ),
),∴过点P的切线方程为:
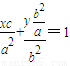 ,
,令y=0,得x=
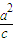 ,
,∴A
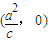 .
.故答案为:
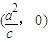 .
.点评:本小题主要考查椭圆的简单性质、椭圆的切线等基础知识,考查运算求解能力,考查数形结合思想,属于基础题.

练习册系列答案
相关题目

 的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线
的右焦点为F,过F的直线(非x轴)交椭圆于M、N两点,右准线 交x轴于点K,左顶点为A.
交x轴于点K,左顶点为A.  ,试用
,试用 的右焦点为F,上顶点为A,P为C
的右焦点为F,上顶点为A,P为C 上任一点,MN是圆
上任一点,MN是圆 的一条直径,若与AF平行且在y轴上的截距为
的一条直径,若与AF平行且在y轴上的截距为 的直线
的直线 恰好与圆
恰好与圆 相切.
相切. 的离心率;
的离心率; 的最大值为49,求椭圆C
的最大值为49,求椭圆C