题目内容
【题目】已知![]() 为椭圆
为椭圆![]()
![]() 的左、右焦点,离心率为
的左、右焦点,离心率为![]() ,点
,点![]() 在椭圆上.
在椭圆上.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 分别交椭圆于
分别交椭圆于![]() 和
和![]() ,且
,且![]() ,问是否存在常数
,问是否存在常数![]() ,使得
,使得![]() 成等差数列?若存在,求出
成等差数列?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
(1)由条件建立关于![]() 的方程组,可求得
的方程组,可求得![]() ,得出椭圆的方程;
,得出椭圆的方程;
(2)①当直线![]() 的斜率不存在时,可求得
的斜率不存在时,可求得![]() ,求得
,求得![]() ,②当直线
,②当直线![]() 的斜率存在且不为0时,设
的斜率存在且不为0时,设![]() 联立直线与椭圆的方程,求出线段
联立直线与椭圆的方程,求出线段![]() ,再由
,再由![]() 得出线段
得出线段![]() ,根据等差中项可求得
,根据等差中项可求得![]() ,得出结论.
,得出结论.
(1)由条件得 ,所以椭圆
,所以椭圆![]() 的方程为:
的方程为:![]() ;
;
(2)![]() ,
,
①当直线![]() 的斜率不存在时,
的斜率不存在时,![]() ,此时
,此时![]() ,
,
②当直线![]() 的斜率存在且不为0时,设
的斜率存在且不为0时,设![]() ,联立
,联立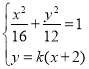 消元得
消元得![]() ,
,
设![]() ,
,![]()
![]() ,
,
![]() 直线
直线![]() 的斜率为
的斜率为![]() ,同理可得
,同理可得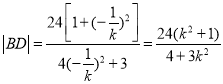
![]() ,
,
![]() 所以
所以![]() ,
,
综合①②,存在常数![]() ,使得
,使得![]() 成等差数列.
成等差数列.

 阅读快车系列答案
阅读快车系列答案【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险的基准保费为a元,在下一年续保时,实行费率浮动机制,保费与车辆发生道路交通事故出险的情况相联系,最终保费![]() 基准保费
基准保费![]() (
(![]() 与道路交通事故相联系的浮动比率),具体情况如下表:
与道路交通事故相联系的浮动比率),具体情况如下表:
交强险浮动因素和浮动费率比率表 | ||
类别 | 浮动因素 | 浮动比率 |
| 上一个年度未发生有责任道路交通事故 | 下浮 |
| 上两个年度未发生有责任道路交通事故 | 下浮 |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮 |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及两次以上有责任不涉及死亡的道路交通事故 | 上浮 |
| 上一个年度发生有责任道路交通死亡事故 | 上浮 |
为了解某一品牌普通6座以下私家车的投保情况,随机抽取了100辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计如下表:
类型 |
|
|
|
|
|
|
数量 | 20 | 10 | 10 | 38 | 20 | 2 |
若以这100辆该品牌的投保类型的频率代替一辆车投保类型的概率,则随机抽取一辆该品牌车在第四年续保时的费用的期望为( )
A.a元B.![]() 元C.
元C.![]() 元D.
元D.![]() 元
元