题目内容
【题目】已知直线![]() ,
,![]() .若
.若![]() ,
,![]() 与两坐标轴围成的四边形有一个外接圆,则
与两坐标轴围成的四边形有一个外接圆,则![]() ________.
________.
【答案】![]() .
.
【解析】
由l1,l2与两坐标轴围成的四边形有一个外接圆,可得此四边形存在一组对角的和等于180°.当直线l2的斜率大于零时,根据l1⊥l2 ,由此求得k的值.当直线l2的斜率小于零时,应有∠ABC与∠ADC互补,即tan∠ABC=﹣tan∠ADC,由此又求得一个k值,综合可得结论.
由题意知,l1,l2与两坐标轴围成的四边形有一组对角互补.
由于直线l1:x+3y﹣5=0是一条斜率等于![]() 的固定直线,直线l2:3kx﹣y+1=0经过定点A(0,1),
的固定直线,直线l2:3kx﹣y+1=0经过定点A(0,1),
当直线l2的斜率大于零时,应有l1⊥l2 ,∴3 k×(![]() )=﹣1,解得 k=1.
)=﹣1,解得 k=1.
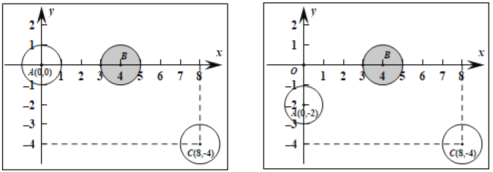
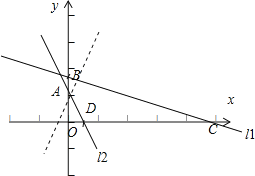
当直线l2的斜率小于零时,如图所示:设直线l1与y轴的交点为B,与x轴的交点为C,l2 与x轴的交点为D,
要使四边形ABCD是圆内接四边形,应有∠ABC与∠ADC互补,即tan∠ABC=﹣tan∠ADC.
再由tan(90°+∠ABC)=KBC![]() ,可得tan∠ABC=3,∴tan∠ADC=﹣3=KAD=3k,解得 k=﹣1.
,可得tan∠ABC=3,∴tan∠ADC=﹣3=KAD=3k,解得 k=﹣1.
综上可得,k=1或 k=﹣1,
故答案为:±1.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目