题目内容
已知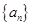 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足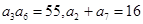 .
.
(1)求数列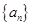 的通项公式;
的通项公式;
(2)若数列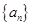 和数列
和数列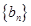 满足等式:
满足等式: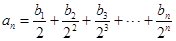 (n为正整数)求数列
(n为正整数)求数列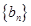 的前n项和
的前n项和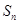 .
.
(1)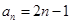 ;(2)
;(2)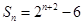
解析试题分析:(1)由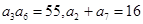 ,根据等差数列的性质将
,根据等差数列的性质将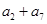 换成
换成 再解方程组即可得到
再解方程组即可得到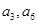 .即可得到通项公式.
.即可得到通项公式.
(2)由(1)可得数列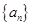 的通项公式,根据已知条件即可求出
的通项公式,根据已知条件即可求出 .当
.当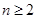 时利用递推一项即可得到数列
时利用递推一项即可得到数列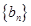 的通项公式,由此得到一个分段的数列
的通项公式,由此得到一个分段的数列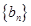 .再根据
.再根据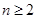 时求出前n项和,再验证n=1是否成立,即可得到结论.
时求出前n项和,再验证n=1是否成立,即可得到结论.
(1){an}是一个公差大于0的等差数列,且满足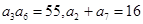 .
.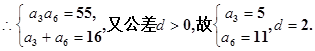
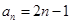 4分
4分
(2)n≥2时,
∴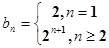 8分
8分
n≥2时,Sn="(4+8+" +2n+1)-2=
n=1时也符合,故Sn=2n+2-6 12分
考点:1.等差数列的性质.2.递推的数学思想.3.等比数列的性质.4.分类的思想.

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,
,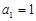 ,
, 是
是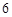 与
与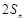 的等差中项(
的等差中项(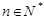 ).
).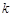 ,使不等式
,使不等式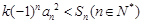 恒成立,若存在,求出
恒成立,若存在,求出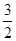 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.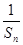 (n∈N*),求数列{Tn}的最大项的值与最小项的值.
(n∈N*),求数列{Tn}的最大项的值与最小项的值.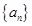 的前
的前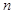 项和记为
项和记为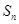 ,
,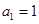 ,
,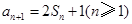 .
.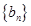 的各项为正,其前
的各项为正,其前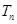 ,且
,且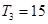 ,又
,又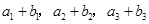 成等比数列,求
成等比数列,求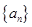 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项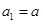 ,
,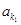 、
、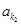 、…、
、…、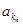 恰为等比数列,且
恰为等比数列,且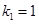 ,
,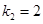 ,
,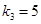 .
. (用
(用 表示);
表示); 的前
的前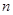 项和为
项和为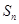 ,求
,求 的前
的前 项和为
项和为 ,向量
,向量 ,(
,( )满足
)满足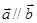 .
. 的通项公式为
的通项公式为 (
( ),若
),若 ,
, ,
, (
( )成等差数列,求
)成等差数列,求 和
和 的值;
的值; 满足
满足 ,公比
,公比 满足
满足 ,且对任意正整数
,且对任意正整数 ,
, 仍是该数列中的某一项,求公比
仍是该数列中的某一项,求公比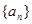 是一个等差数列且
是一个等差数列且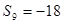 ,
,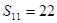 ,
, 项和
项和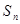 的最小值.
的最小值.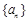 中各项为正数,
中各项为正数,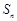 为其前n项和,对任意
为其前n项和,对任意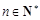 ,总有
,总有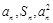 成等差数列.
成等差数列.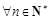 ,
,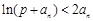 ”是真命题?若存在,求出p;若不存在,请说明理由.
”是真命题?若存在,求出p;若不存在,请说明理由.