题目内容
若关于x的不等式|x-1|-|x-2|≥a2+a+1(x∈R)的解集为空集,则实数a的取值范围为( )A.(0,1)
B.(-1,0)
C.(-∞,-1)
D.(-∞,-1)∪(0,+∞)
【答案】分析:依题意,关于x的不等式|x-1|-|x-2|≥a2+a+1(x∈R)的解集为空集?a2+a+1>|x-1|-|x-2|恒成立,构造函数f(x)=|x-1|-|x-2|,可求其最大值,从而可解关于a的不等式即可.
解答:解:∵|x-1|-|x-2|≥a2+a+1(x∈R)的解集为空集,
∴a2+a+1>|x-1|-|x-2|恒成立,
构造函数f(x)=|x-1|-|x-2|=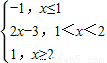 ,
,
则a2+a+1>f(x)max,
∵f(x)max=1,
∴a2+a+1>1,
∴a2+a>0,解得a>0或a<-1.
∴实数a的取值范围为(-∞,-1)∪(0,+∞)
故选D.
点评:本题考查绝对值不等式的解法,考查函数恒成立问题,突出等价转化思想的应用与一元二次不等式的解法的考查,属于中档题.
解答:解:∵|x-1|-|x-2|≥a2+a+1(x∈R)的解集为空集,
∴a2+a+1>|x-1|-|x-2|恒成立,
构造函数f(x)=|x-1|-|x-2|=
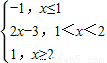 ,
,则a2+a+1>f(x)max,
∵f(x)max=1,
∴a2+a+1>1,
∴a2+a>0,解得a>0或a<-1.
∴实数a的取值范围为(-∞,-1)∪(0,+∞)
故选D.
点评:本题考查绝对值不等式的解法,考查函数恒成立问题,突出等价转化思想的应用与一元二次不等式的解法的考查,属于中档题.

练习册系列答案
相关题目
 A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是:
A.(不等式选做题)若关于x的不等式|x+3|-|x+2|≥log2a有解,则实数a的取值范围是: