题目内容
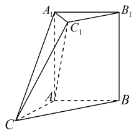
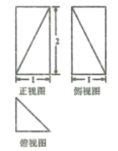
【题目】某四棱锥的三视图如图所示，则它的体积为_______，表面积为_______
【答案】
【解析】
根据三视图可知，该四棱锥是底面为等腰直角三角形，高为2的直三棱柱，截去一个同底等高的的三棱锥所得部分，其体积利用三棱柱的体积减去截去三棱锥的体积求解.表面积根据各面的形状，利用三视图提供的数据，求得各面的面积再求和.
由三视图可知，该四棱锥是底面为等腰直角三角形，高为2的直三棱柱，截去一个同底等高的的三棱锥所得部分，如图所示：
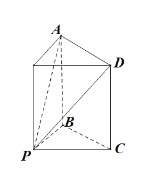
所以该四棱锥P-ABCD的体积为：
，
在矩形ABCD中，AB=2，BC=
，所以S矩形ABCD=
，
在
中，
，所以
，
在
中，
，所以
，
在
中，
，所以
，
在
中，
，
所以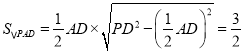
，
所以该四棱锥P-ABCD表面积为：
S= S矩形ABCD
，
故答案为：①；②
练习册系列答案
相关题目
