题目内容
在△ABC中,已知角A,B,C所对的边依次为a,b,c,且2lg(sinB)=lg(sinA)+lg(sinC),则两条直线l1:xsinA+ysinB=a与l2:xsinB+ysinC=c的位置关系是 .
【答案】分析:由对数的运算性质可知sin2B=sinA•sinC,再利用比例关系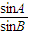 =
=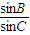 ≠
≠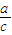 即可判断两直线的位置关系.
即可判断两直线的位置关系.
解答:解:依题意,sin2B=sinA•sinC,
∴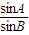 =
=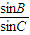 ,即两直线方程中x的系数之比与y的系数之比相等,
,即两直线方程中x的系数之比与y的系数之比相等,
∴两条直线l1:xsinA+ysinB=a与l2:xsinB+ysinC=c平行或重合.
故答案为:平行或重合.
点评:本题考查直线的一般式方程与直线的性质,着重考查两直线方程中x的系数之比与y的系数之比的关系的应用,属于中档题.
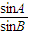 =
=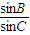 ≠
≠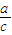 即可判断两直线的位置关系.
即可判断两直线的位置关系.解答:解:依题意,sin2B=sinA•sinC,
∴
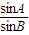 =
=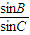 ,即两直线方程中x的系数之比与y的系数之比相等,
,即两直线方程中x的系数之比与y的系数之比相等,∴两条直线l1:xsinA+ysinB=a与l2:xsinB+ysinC=c平行或重合.
故答案为:平行或重合.
点评:本题考查直线的一般式方程与直线的性质,着重考查两直线方程中x的系数之比与y的系数之比的关系的应用,属于中档题.

练习册系列答案
相关题目