题目内容
已知正四面体ABCD中,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
A. | B.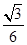 | C.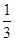 | D. |
B
解析试题分析:设AD的中点为F,连接EF,CE则EF∥BD,所以异面直线CE与EF所成的夹角就是CE与BD所成的夹角,设正四面体ABCD的棱长为2a,则EF=a,CE=CF=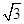 a,由余弦定理可得cos∠CEF=
a,由余弦定理可得cos∠CEF= ,故选B.
,故选B.
考点:正多面体的性质和异面直线的夹角以及余弦定理.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
过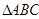 所在平面
所在平面 外一点
外一点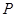 ,作
,作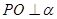 ,垂足为
,垂足为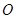 ,连接
,连接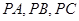 .若
.若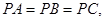 则点
则点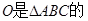 ( )
( )
| A.垂心 | B.外心 | C.内心 | D.重心 |
设m,n是两条不同的直线,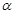 、
、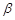 、
、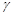 是三个不同的平面,给出下列命题,正确的是( ).
是三个不同的平面,给出下列命题,正确的是( ).
A.若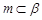 , ,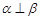 ,则 ,则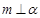 | B.若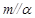 , ,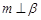 ,则 ,则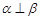 |
C.若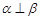 , ,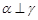 ,则 ,则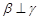 | D.若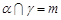 , ,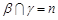 , ,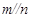 ,则 ,则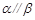 |
设 是不同的直线,
是不同的直线,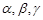 是不同的平面,有以下四个命题:
是不同的平面,有以下四个命题:
①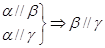 ②
②
③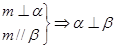 ④
④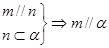
其中,真命题是( )
| A.①④ | B.②③ | C.①③ | D.②④ |
以下说法中,正确的个数是( )
①平面 内有一条直线和平面
内有一条直线和平面 平行,那么这两个平面平行
平行,那么这两个平面平行
②平面 内有两条直线和平面
内有两条直线和平面 平行,那么这两个平面平行
平行,那么这两个平面平行
③平面 内有无数条直线和平面
内有无数条直线和平面 平行,那么这两个平面平行
平行,那么这两个平面平行
④平面 内任意一条直线和平面
内任意一条直线和平面 都无公共点,那么这两个平面平行
都无公共点,那么这两个平面平行
| A.0个 | B.1个 | C.2个 | D.3个 |
已知两条直线m,n,两个平面α,β.给出下面四个命题:
①m∥n,m⊥α⇒n⊥α;
②α∥β,m?α,n?β⇒m∥n;
③m∥n,m∥α⇒n∥α;
④α∥β,m∥n,m⊥α⇒n⊥β.
其中正确命题的序号是( )
| A.①③ | B.②④ | C.①④ | D.②③ |
在正方体ABCD-A1B1C1D1中,点M,N分别在线段AB1,BC1上,且AM=BN.以下结论:①AA1⊥MN;②A1C1∥MN;③MN∥平面A1B1C1D1;④MN与A1C1异面,其中有可能成立的个数为( )
| A.4 | B.3 | C.2 | D.1 |
(2014·黄冈模拟)设a,b是平面α内两条不同的直线,l是平面α外的一条直线,则“l⊥a,l⊥b”是“l⊥α”的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
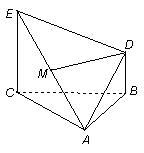
 为正三角形,EC
为正三角形,EC
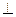 平面ABC,BD
平面ABC,BD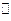 CE,且CE=CA=2BD=a,M是EA的中点.(1)求证:(1) DM
CE,且CE=CA=2BD=a,M是EA的中点.(1)求证:(1) DM