题目内容
已知函数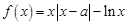 ,
,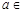
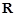 .
.
(Ⅰ)若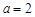 ,求函数
,求函数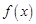 在区间
在区间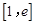 上的最值;
上的最值;
(Ⅱ)若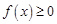 恒成立,求
恒成立,求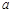 的取值范围. (注:
的取值范围. (注: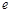 是自然对数的底数)
是自然对数的底数)
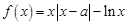 ,
,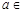
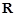 .
.(Ⅰ)若
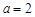 ,求函数
,求函数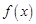 在区间
在区间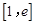 上的最值;
上的最值;(Ⅱ)若
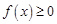 恒成立,求
恒成立,求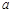 的取值范围. (注:
的取值范围. (注: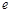 是自然对数的底数)
是自然对数的底数)(Ⅰ) 最大值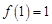 ;(Ⅱ)
;(Ⅱ)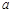 的取值范围是
的取值范围是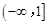 .
.
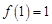 ;(Ⅱ)
;(Ⅱ)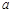 的取值范围是
的取值范围是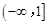 .
.试题分析:(Ⅰ) 讨论去掉绝对值,利用导数求得最值; (Ⅱ) 对
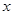 分
分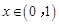 ,
,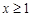 讨论:当
讨论:当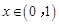 时
时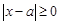 ,
,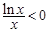 ,
,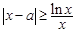 恒成立,所以
恒成立,所以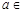
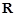 ;当
;当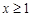 时,对
时,对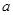 讨论去掉绝对值,分离出
讨论去掉绝对值,分离出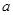 通过求函数的最值求得
通过求函数的最值求得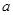 的范围.
的范围.试题解析:(1) 若
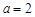 ,则
,则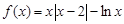 .当
.当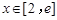 时,
时,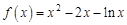 ,
,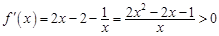 , 所以函数
, 所以函数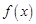 在
在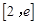 上单调递增;
上单调递增;当
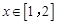 时,
时,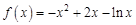 ,
,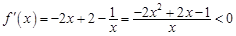 .
.所以函数
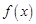 在区间
在区间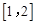 上单调递减,所以
上单调递减,所以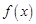 在区间[1,e]上有最小值
在区间[1,e]上有最小值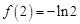 ,又因为
,又因为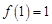 ,
,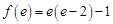 ,而
,而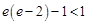 ,所以
,所以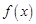 在区间
在区间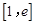 上有最大值
上有最大值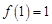 .
.(2)函数
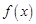 的定义域为
的定义域为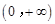 . 由
. 由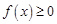 ,得
,得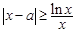 . (*)
. (*)(ⅰ)当
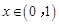 时,
时,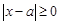 ,
,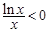 ,不等式(*)恒成立,所以
,不等式(*)恒成立,所以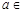
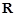 ;
;(ⅱ)当
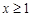 时,
时,①当
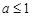 时,由
时,由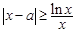 得
得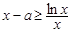 ,即
,即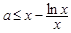 ,
,现令
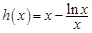 , 则
, 则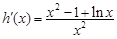 ,因为
,因为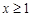 ,所以
,所以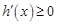 ,故
,故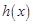 在
在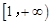 上单调递增,
上单调递增,从而
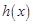 的最小值为
的最小值为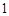 ,因为
,因为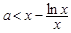 恒成立等价于
恒成立等价于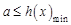 ,所以
,所以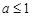 ;
;②当
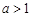 时,
时,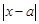 的最小值为
的最小值为 ,而
,而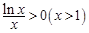 ,显然不满足题意.
,显然不满足题意.综上可得,满足条件的
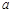 的取值范围是
的取值范围是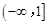 .
. 
练习册系列答案
相关题目
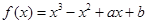 .
.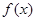 在
在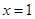 处取得极值,且函数
处取得极值,且函数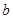 的取值范围.
的取值范围.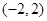 上不是单调函数,求
上不是单调函数,求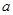 的取值范围.
的取值范围. ,
, ,且
,且 在点(1,
在点(1, )处的切线方程为
)处的切线方程为 。
。 的单调递增区间;
的单调递增区间; ,若方程
,若方程 有且仅有四个解,求实数a的取值范围。
有且仅有四个解,求实数a的取值范围。 .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;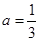 时,求函数
时,求函数 ,若对于
,若对于 [1,2],
[1,2], [0,1],使
[0,1],使 成立,求实数
成立,求实数 的取值范围.
的取值范围.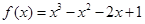 相切的直线有 条(以数字作答).
相切的直线有 条(以数字作答). 处的切线与坐标轴围成的三角形面积为( )
处的切线与坐标轴围成的三角形面积为( )



 在
在 处的切线平行于直线
处的切线平行于直线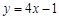 ,则
,则 的图像在点
的图像在点 处的切线斜率为
处的切线斜率为 ,则
,则 的值是 .
的值是 .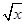 与
与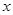 轴及直线
轴及直线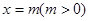 围成的图形面积为
围成的图形面积为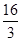 ,则
,则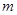 的值为 .
的值为 .