题目内容
已知以 为周期的函数
为周期的函数 ,其中
,其中 。若方程
。若方程 恰有5个实数解,则
恰有5个实数解,则 的取值范围为
的取值范围为

解析试题分析:据对函数的解析式进行变形后发现当x∈(-1,1],[3,5],[7,9]上时,f(x)的图象为半个椭圆.根据图象推断要使方程恰有5个实数解,则需直线y=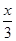 与第二个椭圆相交,而与第三个椭圆不公共点.把直线分别代入椭圆方程,根据△可求得m的范围。解:∵当x∈(-1,1]时,将函数化为方程
与第二个椭圆相交,而与第三个椭圆不公共点.把直线分别代入椭圆方程,根据△可求得m的范围。解:∵当x∈(-1,1]时,将函数化为方程 (y≥0),∴实质上为一个半椭圆,其图象如图所示,同时在坐标系中作出当x∈(1,3]得图象,再根据周期性作出函数其它部分的图象,由图易知直线 y=
(y≥0),∴实质上为一个半椭圆,其图象如图所示,同时在坐标系中作出当x∈(1,3]得图象,再根据周期性作出函数其它部分的图象,由图易知直线 y=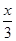 与第二个椭圆
与第二个椭圆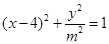 相交,而与第三个半椭圆
相交,而与第三个半椭圆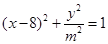 无公共点时,方程恰有5个实数解,将y=
无公共点时,方程恰有5个实数解,将y=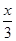 代入
代入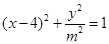 中得到,,(9m2+1)x2-72m2x+135m2=0,令t=9m2(t>0),则(t+1)x2-8tx+15t=0,由△=(8t)2-4×15t (t+1)>0,得t>15,由9m2>15,且m>0得 m >
中得到,,(9m2+1)x2-72m2x+135m2=0,令t=9m2(t>0),则(t+1)x2-8tx+15t=0,由△=(8t)2-4×15t (t+1)>0,得t>15,由9m2>15,且m>0得 m > ,同样由y=
,同样由y=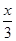 代入
代入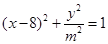 由△<0可计算得 m<
由△<0可计算得 m<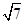 ,故可知m的范围
,故可知m的范围
考点:函数与方程
点评:解决的关键是利用函数的周期性以及方程的解的运用,属于中档题。

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
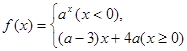 为减函数,则a的取值范围是
为减函数,则a的取值范围是  时,
时, 的值为3,则当
的值为3,则当 时,
时, 的值为 .
的值为 . 的单调增区间为 .
的单调增区间为 .  满足:任意的
满足:任意的 ,都有
,都有 ,且
,且 时,
时, ,则函数
,则函数 的所有零点之和为 .
的所有零点之和为 .  在区间(0,1]上是减函数,则
在区间(0,1]上是减函数,则 的取值范围是_________。
的取值范围是_________。 的定义域为 .
的定义域为 . 的单调递减区间 .
的单调递减区间 .  的定义域为
的定义域为 ,若
,若 时,
时,
