题目内容
已知函数f(x)=(m+1)x2-(m-1)x+m-1(1)若不等式f(x)<1的解集为R,求m的取值范围;
(2)解关于x的不等式f(x)≥(m+1)x;
(3)若不等式f(x)≥0对一切
 恒成立,求m的取值范围.
恒成立,求m的取值范围.
【答案】分析:(1)对二次项系数m+1的情况分类讨论,由不等式f(x)<1的解集为R,可得 ,解之即可求得m的取值范围;
,解之即可求得m的取值范围;
(2)f(x)≥(m+1)x?[(m+1)x-(m-1)](x-1)≥0,对m+1=0,m+1>0与m+1<0分类讨论,可分别求得其解集;
(3)(m+1)x2-(m-1)x+m-1≥0?m(x2-x+1)≥-x2-x+1?m≥ ,通过分离常数与利用基本不等式结合已知即可求得m的取值范围.
,通过分离常数与利用基本不等式结合已知即可求得m的取值范围.
解答:解:(1)①当m+1=0即m=-1时,f(x)=2x-3,不合题意; …(1分)
②当m+1≠0即m≠-1时, ,即
,即 ,…(3分)
,…(3分)
∴ ,
,
∴m< …(5分)
…(5分)
(2)f(x)≥(m+1)x即(m+1)x2-2mx+m-1≥0
即[(m+1)x-(m-1)](x-1)≥0
①当m+1=0即m=-1时,解集为{x|x≥1}…(7分)
②当m+1>0即m>-1时,(x- )(x-1)≥0,
)(x-1)≥0,
∵ =1-
=1- <1,
<1,
∴解集为{x|x≤ 或x≥1}…(9分)
或x≥1}…(9分)
③当m+1<0即m<-1时,(x- )(x-1)≥0,
)(x-1)≥0,
∵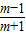 =1-
=1- >1,
>1,
∴解集为{x|x≥ 或x≤1}…(…(11分)
或x≤1}…(…(11分)
(3)(m+1)x2-(m-1)x+m-1≥0,即m(x2-x+1)≥-x2-x+1,
∵x2-x+1>0恒成立,
∴m≥ =-1+
=-1+ …(13分)
…(13分)
设1-x=t,则t∈[ ,
, ],x=1-t,
],x=1-t,
∴ =
= =
= =
= ,
,
∵t+ ≥2,当且仅当t=1时取等号,
≥2,当且仅当t=1时取等号,
∴ ≤1,当且仅当x=0时取等号,
≤1,当且仅当x=0时取等号,
∴当x=0时, =1,
=1,
∴m≥1…(16分)
点评:本题考查函数恒成立问题,突出考查二次函数的性质及一元二次不等式的解法,突出分类讨论思想与构造函数思想及比较大小方法的综合应用,属于难题.
 ,解之即可求得m的取值范围;
,解之即可求得m的取值范围;(2)f(x)≥(m+1)x?[(m+1)x-(m-1)](x-1)≥0,对m+1=0,m+1>0与m+1<0分类讨论,可分别求得其解集;
(3)(m+1)x2-(m-1)x+m-1≥0?m(x2-x+1)≥-x2-x+1?m≥
 ,通过分离常数与利用基本不等式结合已知即可求得m的取值范围.
,通过分离常数与利用基本不等式结合已知即可求得m的取值范围.解答:解:(1)①当m+1=0即m=-1时,f(x)=2x-3,不合题意; …(1分)
②当m+1≠0即m≠-1时,
 ,即
,即 ,…(3分)
,…(3分)∴
 ,
,∴m<
 …(5分)
…(5分)(2)f(x)≥(m+1)x即(m+1)x2-2mx+m-1≥0
即[(m+1)x-(m-1)](x-1)≥0
①当m+1=0即m=-1时,解集为{x|x≥1}…(7分)
②当m+1>0即m>-1时,(x-
 )(x-1)≥0,
)(x-1)≥0,∵
 =1-
=1- <1,
<1,∴解集为{x|x≤
 或x≥1}…(9分)
或x≥1}…(9分)③当m+1<0即m<-1时,(x-
 )(x-1)≥0,
)(x-1)≥0,∵
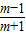 =1-
=1- >1,
>1,∴解集为{x|x≥
 或x≤1}…(…(11分)
或x≤1}…(…(11分)(3)(m+1)x2-(m-1)x+m-1≥0,即m(x2-x+1)≥-x2-x+1,
∵x2-x+1>0恒成立,
∴m≥
 =-1+
=-1+ …(13分)
…(13分)设1-x=t,则t∈[
 ,
, ],x=1-t,
],x=1-t,∴
 =
= =
= =
= ,
,∵t+
 ≥2,当且仅当t=1时取等号,
≥2,当且仅当t=1时取等号,∴
 ≤1,当且仅当x=0时取等号,
≤1,当且仅当x=0时取等号,∴当x=0时,
 =1,
=1,∴m≥1…(16分)
点评:本题考查函数恒成立问题,突出考查二次函数的性质及一元二次不等式的解法,突出分类讨论思想与构造函数思想及比较大小方法的综合应用,属于难题.

练习册系列答案
相关题目
已知函数f(x)=x2-bx的图象在点A(1,f(1))处的切线l与直线3x-y+2=0平行,若数列{
}的前n项和为Sn,则S2010的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|