题目内容
已知数列{an}的前n项和是Sn(n∈N*),a1=1且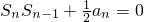
(1)求数列{an}的通项公式;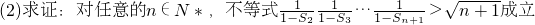 .
.
解:(1)∵a1=1且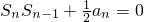
即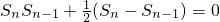 (n≥2)
(n≥2)
2Sn•Sn-1=Sn-1-Sn两边同除以Sn•Sn-1得
2= -
-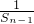 ∴数列{
∴数列{ }是以1为首项,以2为公差的等差数列.
}是以1为首项,以2为公差的等差数列.
∴ =1+2(n-1)=2n-1
=1+2(n-1)=2n-1
∴Sn= ,
,
当n=1时,a1=1,
当n≥2时,an=Sn-Sn-1=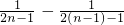 =
=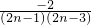
∴an=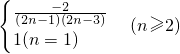
(2)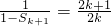
用数学归纳法证明:
当n=1时,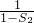 =
=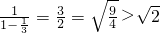 ,不等式成立. ①
,不等式成立. ①
假设当n=k(k≥2)时成立,即有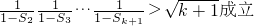
那么当n=k+1时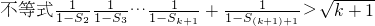
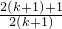 =
=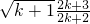
下证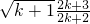 >
>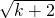 成立.
成立.
只需证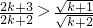
两边平方即为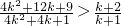 ,两边减去1得
,两边减去1得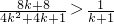
即证8(k+1)2>4k2+4k+1,
即4k2+12k+7>0,显然成立②
由①②可知,原不等式对任意正整数n都成立.
分析:(1)将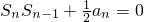 转化为 2Sn•Sn-1=Sn-1-Sn两边同除以Sn•Sn-1得2=
转化为 2Sn•Sn-1=Sn-1-Sn两边同除以Sn•Sn-1得2= -
-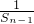 构造数列{
构造数列{ }是以1为首项,以2为公差的等差数列,求其通项公式,再据Sn与an的关系求数列{an}的通项公式
}是以1为首项,以2为公差的等差数列,求其通项公式,再据Sn与an的关系求数列{an}的通项公式
(2)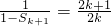 ,不等式左端无法进一步整理化简,又是与自然数有关,考虑用数学归纳法证明.
,不等式左端无法进一步整理化简,又是与自然数有关,考虑用数学归纳法证明.
点评:本题考查通项公式求解、不等式的证明,用到的知识和方法有,Sn与an的关系,数学归纳法,考查分析解决问题、转化、计算等能力.
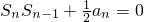
即
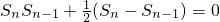 (n≥2)
(n≥2)2Sn•Sn-1=Sn-1-Sn两边同除以Sn•Sn-1得
2=
 -
-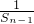 ∴数列{
∴数列{ }是以1为首项,以2为公差的等差数列.
}是以1为首项,以2为公差的等差数列.∴
 =1+2(n-1)=2n-1
=1+2(n-1)=2n-1∴Sn=
 ,
,当n=1时,a1=1,
当n≥2时,an=Sn-Sn-1=
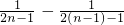 =
=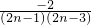
∴an=
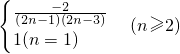
(2)
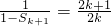
用数学归纳法证明:
当n=1时,
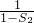 =
=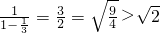 ,不等式成立. ①
,不等式成立. ①假设当n=k(k≥2)时成立,即有
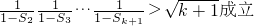
那么当n=k+1时
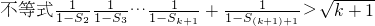
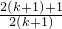 =
=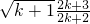
下证
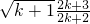 >
>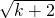 成立.
成立.只需证
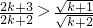
两边平方即为
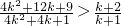 ,两边减去1得
,两边减去1得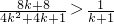
即证8(k+1)2>4k2+4k+1,
即4k2+12k+7>0,显然成立②
由①②可知,原不等式对任意正整数n都成立.
分析:(1)将
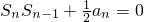 转化为 2Sn•Sn-1=Sn-1-Sn两边同除以Sn•Sn-1得2=
转化为 2Sn•Sn-1=Sn-1-Sn两边同除以Sn•Sn-1得2= -
-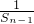 构造数列{
构造数列{ }是以1为首项,以2为公差的等差数列,求其通项公式,再据Sn与an的关系求数列{an}的通项公式
}是以1为首项,以2为公差的等差数列,求其通项公式,再据Sn与an的关系求数列{an}的通项公式(2)
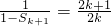 ,不等式左端无法进一步整理化简,又是与自然数有关,考虑用数学归纳法证明.
,不等式左端无法进一步整理化简,又是与自然数有关,考虑用数学归纳法证明.点评:本题考查通项公式求解、不等式的证明,用到的知识和方法有,Sn与an的关系,数学归纳法,考查分析解决问题、转化、计算等能力.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |