题目内容
求适合下列条件的双曲线的标准方程:(1)焦点在 x轴上,虚轴长为12,离心率为
 ;
;(2)顶点间的距离为6,渐近线方程为
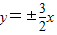 .
.
【答案】分析:(1)由于双曲线的焦点在x轴上,设所求双曲线的方程为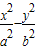 =1.由题意,得出关于a,c的方程组即可解得a,c,结合b2=c2-a2求出b值,写出双曲线的方程即可;
=1.由题意,得出关于a,c的方程组即可解得a,c,结合b2=c2-a2求出b值,写出双曲线的方程即可;
(2)当焦点在x轴上时,设所求双曲线的方程为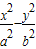 =1得出关于a,b的方程组即可解得a,b,写出双曲线的方程即可;同理可求当焦点在y轴上双曲线的方程.
=1得出关于a,b的方程组即可解得a,b,写出双曲线的方程即可;同理可求当焦点在y轴上双曲线的方程.
解答:解:(1)焦点在x轴上,设所求双曲线的方程为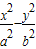 =1.
=1.
由题意,得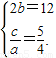 解得a=8,c=10.
解得a=8,c=10.
∴b2=c2-a2=100-64=36.
所以焦点在x轴上的双曲线的方程为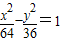 .
.
(2)当焦点在x轴上时,设所求双曲线的方程为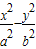 =1
=1
由题意,得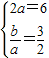 解得a=3,b=2.
解得a=3,b=2.
所以焦点在x轴上的双曲线的方程为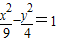 .
.
同理可求当焦点在y轴上双曲线的方程为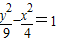 .
.
点评:本小题主要考查双曲线的标准方程、双曲线的简单性质等基础知识,求双曲线的标准方程,先确定标准方程的形式,再根据条件求出 a,b.
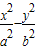 =1.由题意,得出关于a,c的方程组即可解得a,c,结合b2=c2-a2求出b值,写出双曲线的方程即可;
=1.由题意,得出关于a,c的方程组即可解得a,c,结合b2=c2-a2求出b值,写出双曲线的方程即可;(2)当焦点在x轴上时,设所求双曲线的方程为
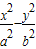 =1得出关于a,b的方程组即可解得a,b,写出双曲线的方程即可;同理可求当焦点在y轴上双曲线的方程.
=1得出关于a,b的方程组即可解得a,b,写出双曲线的方程即可;同理可求当焦点在y轴上双曲线的方程.解答:解:(1)焦点在x轴上,设所求双曲线的方程为
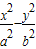 =1.
=1.由题意,得
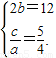 解得a=8,c=10.
解得a=8,c=10.∴b2=c2-a2=100-64=36.
所以焦点在x轴上的双曲线的方程为
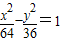 .
.(2)当焦点在x轴上时,设所求双曲线的方程为
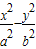 =1
=1由题意,得
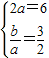 解得a=3,b=2.
解得a=3,b=2.所以焦点在x轴上的双曲线的方程为
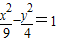 .
.同理可求当焦点在y轴上双曲线的方程为
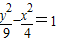 .
.点评:本小题主要考查双曲线的标准方程、双曲线的简单性质等基础知识,求双曲线的标准方程,先确定标准方程的形式,再根据条件求出 a,b.

练习册系列答案
相关题目
 、
、 且过点
且过点
 椭圆;
椭圆; 有相同的渐近线,且过点
有相同的渐近线,且过点 的双曲线.
的双曲线.