Question

8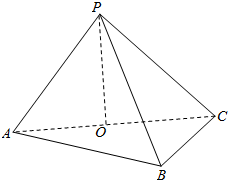．P为△ABC所在平面外一点，PO⊥面ABC于O．证明：
（1）若PA=PB=PC，则O为△ABC的外心；
（2）若PA⊥BC，PC⊥AB，则PB⊥AC，且O为△ABC的垂心；
（3）若PA，PB，PC两两垂直，则O为△ABC的垂心；
（4）若P到△ABC各边的距离相等（且O在三角形的内部），则O为△ABC的内心．

Answer 1

分析 （1）由PA=PB=PC，利用射影定理得OA=OB=OC，由此能证明O为△ABC的外心．
（2）由知推导出BC⊥平面PAC，从而OA⊥BC，同理OB⊥AC，由此能证明O是△ABC的垂心，从而得到PB⊥AC．
（3）连接AO，BO，CO，由已知推导出PA⊥平面PBC，从而PA⊥BC，进而得到BC⊥AO同理，BO⊥AC，CO⊥AB，由此能证明O为△ABC的垂心．
（4）由射影定理得O到△ABC三边距离相等，由此能证明O是△ABC的内心．

解答 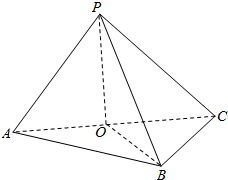证明：（1）∵P为△ABC所在平面外一点，PO⊥面ABC于O，
PA=PB=PC，
∴由射影定理得OA=OB=OC，
∴O为△ABC的外心．
（2）∵P为△ABC所在平面外一点，PO⊥面ABC于O，
PA⊥BC，PC⊥AB，
∴PO⊥BC，PA⊥BC，
∵PO∩PA=P，∴BC⊥平面PAC，∴OA⊥BC，
同理OB⊥AC，
∴O是△ABC的垂心，
∴OC⊥AB，又PO⊥AB，OC∩PO=O，
∴AB⊥平面PAC，∴PB⊥AC，
∴PB⊥AC，且O为△ABC的垂心．
（3）P为△ABC所在平面外一点，PO⊥面ABC于O，
PA，PB，PC两两垂直，
连接AO，BO，CO
∵PA⊥PB，PA⊥PC，∴PA⊥平面PBC，∴PA⊥BC，
∵PO⊥平面ABC，∴PO⊥BC，PO∩PA=P，
∴BC⊥平面PAO，∴BC⊥AO
同理，BO⊥AC，CO⊥AB，
∴O为△ABC的垂心．
（4）∵P为△ABC所在平面外一点，PO⊥面ABC于O，
P到△ABC三边距离相等，且O在△ABC的内部，
∴由射影定理得O到△ABC三边距离相等，
∴O是△ABC的内心．

点评 本题考查三角形五心的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．