题目内容

设点A为圆（x-1）2+y2=1上的动点，PA是圆的切线，且|PA|=1，则P点的轨迹方程为（　　）
分析：圆（x-1）2+y2=1的圆心为C（1，0），半径为1，根据PA是圆的切线，且|PA|=1，可得|PC|=
2
，从而可求P点的轨迹方程
解答：解：设P（x，y），则由题意，圆（x-1）2+y2=1的圆心为C（1，0），半径为1
∵PA是圆的切线，且|PA|=1
∴|PC|=
2

∴P点的轨迹方程为（x-1）2+y2=2
故选D．
点评：本题以圆的标准方程为载体，考查圆的切线性质，考查轨迹方程的求解，属于基础题．
练习册系列答案
相关题目
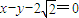（2012•吉林二模）已知圆C1的圆心在坐标原点O，且恰好与直线l1：x-y-2
2
=0相切．
（1）求圆的标准方程；
（2）设点A为圆上一动点，AN⊥x轴于N，若动点Q满足：
OQ
=m
OA
+(1-m)
ON
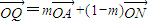，（其中m为非零常数），试求动点Q的轨迹方程C2；
（3）在（2）的结论下，当m=
3
2
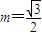时，得到曲线C，与l1垂直的直线l与曲线C交于B、D两点，求△OBD面积的最大值．
（2012•台州一模）设点A在圆x2+y2=1内，点B（t，0），O为坐标原点，若集合{C|
OC
=
OA
+
OB
}⊆{（x，y）|x2+y2≤9}，则实数t的最大值为
2
2
．
已知圆C1的圆心在坐标原点O，且恰好与直线l1：相切．
（1）求圆的标准方程；
（2）设点A为圆上一动点，AN⊥x轴于N，若动点Q满足：，（其中m为非零常数），试求动点Q的轨迹方程C2；
（3）在（2）的结论下，当时，得到曲线C，与l1垂直的直线l与曲线C交于B、D两点，求△OBD面积的最大值．
设点A为圆（x-1）2+y2=1上的动点，PA是圆的切线，且|PA|=1，则P点的轨迹方程为（ ）
A．y2=2
B．（x-1）2+y2=4
C．y2=-2
D．（x-1）2+y2=2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网