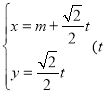题目内容
【题目】设二次函数![]() 满足下列条件:
满足下列条件:
①![]() 对
对![]() 恒成立; ②
恒成立; ②![]() 对
对![]() 恒成立.
恒成立.
(1)求![]() 的值; (2)求
的值; (2)求![]() 的解析式;
的解析式;
(3)求最大的实数![]() ,使得存在实数
,使得存在实数![]() ,当
,当![]() 时,
时, ![]() 恒成立.
恒成立.
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)由当x∈(0,5)时,都有x≤f(x)≤2|x﹣1|+1恒成立可得f(1)=1;
(2)由f(﹣1+x)=f(﹣1﹣x)可得二次函数f(x)=ax2+bx+c(a,b,c∈R)的对称轴为x=﹣1,于是b=2a,再由f(x)min=f(﹣1)=0,可得c=a,从而可求得函数f(x)的解析式;
(3)可由f(1+t)≤1,求得:﹣4≤t≤0,再利用平移的知识求得最大的实数m.
试题解析:
(1)当x=1时, ![]()
(2)由已知可得![]() ……①
……①
由![]() ……②
……②
![]()
由![]() 恒成立
恒成立![]() 对R恒成立
对R恒成立
则![]()
![]()
由![]() 对
对![]() 恒成立
恒成立
![]() 恒成立
恒成立
则![]()

![]() ,
,![]()
(3)![]() 恒成立,则使
恒成立,则使![]() 的图像在
的图像在![]() 的下方,且m最大,则1,m为
的下方,且m最大,则1,m为![]() 的两个根
的两个根
由![]()
![]()
![]()
∴![]() .
.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
【题目】化为推出一款6寸大屏手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户:
分值区间 |
|
|
|
|
|
频数 | 20 | 40 | 80 | 50 | 10 |
分值区间 |
|
|
|
|
|
频数 | 45 | 75 | 90 | 60 | 30 |
男性用户:
(1)如果评分不低于70分,就表示该用户对手机“认可”,否则就表示“不认可”,完成下列![]() 列联表,并回答是否有
列联表,并回答是否有![]() 的把握认为性别对手机的“认可”有关:
的把握认为性别对手机的“认可”有关:
女性用户 | 男性用户 | 合计 | |
“认可”手机 | |||
“不认可”手机 | |||
合计 |
附:
| 0.05 | 0.01 |
| 3.841 | 6635 |
![]()
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意抽取3名用户,求3名用户中评分小于90分的人数的分布列和数学期望.