题目内容
若点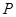 在椭圆
在椭圆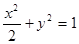 上,
上, 、
、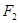 分别是椭圆的两焦点,且
分别是椭圆的两焦点,且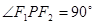 ,则
,则 的面积是
( )
的面积是
( )
A.
2
B. 1 C. 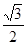 D.
D.
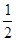
【答案】
B
【解析】略

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 中,已知点
中,已知点 为椭圆
为椭圆 的右顶点, 点
的右顶点, 点 ,点
,点 在椭圆上,
在椭圆上,  .
. 的方程; (2)求直线
的方程; (2)求直线 三点的圆
三点的圆 截得的弦长;
截得的弦长; 为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不
为弦的两个相外切的等圆?若存在,求出这两个圆的方程;若不
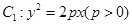 的焦点
的焦点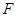 以及椭圆
以及椭圆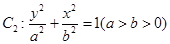 的上、下焦点及左、右顶点均在圆
的上、下焦点及左、右顶点均在圆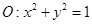 上.
上.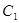 和椭圆
和椭圆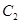 的标准方程;
的标准方程;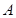 、
、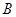 两不同点,交
两不同点,交 轴于点
轴于点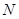 ,已知
,已知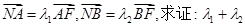 为定值.
为定值. 交椭圆
交椭圆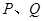 两不同点,
两不同点,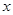 轴的射影分别为
轴的射影分别为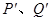 ,
, ,若点
,若点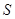 满足:
满足: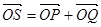 ,证明:点
,证明:点 :
: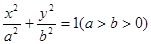 ,
, 分别为左,右焦点,离心率为
分别为左,右焦点,离心率为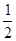 ,点
,点 在椭圆
在椭圆 ,
, ,过
,过 与坐标轴不垂直的直线
与坐标轴不垂直的直线 交椭圆于
交椭圆于 两点.
两点. 上是否存在点
上是否存在点 ,使得以线段
,使得以线段 为邻边的四边形是菱形?若存在,求出实数
为邻边的四边形是菱形?若存在,求出实数 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由. 的左、右焦点分别为
的左、右焦点分别为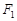 、
、 ,点
,点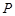 在双曲线的右支上,直线
在双曲线的右支上,直线 为过
为过 ,过
,过 作与直线
作与直线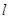 平行的直线交
平行的直线交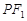 于
于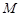 点,则
点,则 ,利用类比推理:若椭圆
,利用类比推理:若椭圆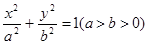 的左、右焦点分别为
的左、右焦点分别为 的值为 ( )
的值为 ( ) 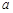 (B)
(B) (C)
(C) (D)无法确定[来
(D)无法确定[来