题目内容
已知定点A(-2,0),B(2,0),曲线E上任一点P满足|PA|-|PB|=2.
(1)求曲线E的方程;
(2)延长PB与曲线E交于另一点Q,求|PQ|的最小值;
(3)若直线l的方程为x=a(a≤
),延长PB与曲线E交于另一点Q,如果存在某一位置,使得PQ的中点R在l上的射影C满足PC⊥QC,求a的取值范围.
(1)求曲线E的方程;
(2)延长PB与曲线E交于另一点Q,求|PQ|的最小值;
(3)若直线l的方程为x=a(a≤
| 1 | 2 |
分析:(1)由题意可知P点轨迹为双曲线,由a,c求出b的值,则方程可求;
(2)当直线斜率存在时,设出直线方程,和双曲线方程联立后求得判别式大于0,再由两根之和大于0,且两根之积大于0联立求得k的范围由弦长公式写出弦长,借助于k的范围求弦长的范围,当斜率不存在时直接求解;
(3)由题意可知P、C、Q构成直角三角形,求出R到直线l的距离|RC|=
=xR-a,由点P、Q都在双曲线x2-
=1上,借助于双曲线的第二定义得到
=
=2,利用合比定理得到xR=
,与
R到直线l的距离联立可得答案.
(2)当直线斜率存在时,设出直线方程,和双曲线方程联立后求得判别式大于0,再由两根之和大于0,且两根之积大于0联立求得k的范围由弦长公式写出弦长,借助于k的范围求弦长的范围,当斜率不存在时直接求解;
(3)由题意可知P、C、Q构成直角三角形,求出R到直线l的距离|RC|=
| |PQ| |
| 2 |
| y2 |
| 3 |
| |PB| | ||
xp-
|
| |QB| | ||
xQ-
|
| |PQ|+2 |
| 4 |
R到直线l的距离联立可得答案.
解答:(1)解:∵|PA|-|PB|=2,
∴点P的轨迹是以A、B为焦点,焦距为4,实轴长为2的双曲线的右支,
则a=1,c=2,∴b2=c2-a2=3.
其方程为x2-
=1(x≥1);
(2)若直线PQ的斜率存在,设斜率为k,则直线PQ的方程为y=k(x-2)代入双曲线方程,
得(3-k2)x2+4k2x-4k2-3=0,
由△>0,
,解得k2>3,
∴|PQ|=
|x1-x2|=
=6+
>6
当直线斜率不存在时,x1=x2=2,得y1=3,y2=-3,|PQ|=6,|PQ|的最小值为6
(3)当PC⊥CQ时,P、C、Q构成直角三角形
∴R到直线l的距离|RC|=
=xR-a①
又∵点P、Q都在双曲线x2-
=1上,
∴
=
=2,
∴
=2,即|PQ|=4xR-2,∴xR=
②
将②代入①得
=
-a,|PQ|=2-4a≥6,
故有a≤-1.
∴点P的轨迹是以A、B为焦点,焦距为4,实轴长为2的双曲线的右支,
则a=1,c=2,∴b2=c2-a2=3.
其方程为x2-
| y2 |
| 3 |
(2)若直线PQ的斜率存在,设斜率为k,则直线PQ的方程为y=k(x-2)代入双曲线方程,
得(3-k2)x2+4k2x-4k2-3=0,
由△>0,
|
∴|PQ|=
| 1+k2 |
| 6(k2+1) |
| k2-3 |
| 24 |
| k2-3 |
当直线斜率不存在时,x1=x2=2,得y1=3,y2=-3,|PQ|=6,|PQ|的最小值为6
(3)当PC⊥CQ时,P、C、Q构成直角三角形
∴R到直线l的距离|RC|=
| |PQ| |
| 2 |
又∵点P、Q都在双曲线x2-
| y2 |
| 3 |
∴
| |PB| | ||
xp-
|
| |QB| | ||
xQ-
|
∴
| |PB|+|QB| |
| xp+xQ-1 |
| |PQ|+2 |
| 4 |
将②代入①得
| |PQ| |
| 2 |
| |PQ|+2 |
| 4 |
故有a≤-1.
点评:本题考查了双曲线的方程,考查了直线与圆锥曲线的关系,训练了弦长公式的用法,双曲线的第二定义是解答(3)的关键,考查了学生综合处理问题的能力和计算能力,是较难的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
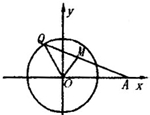 如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.
如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.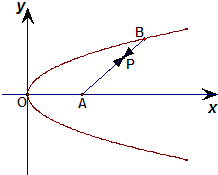 如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得
如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得