题目内容
已知定点A(-2,0),动点B是圆F:(x-2)2+y2=64(F为圆心)上一点,线段AB的垂直平分线交BF于P;(1)求动点P的轨迹E的方程;
(2)直线y=
| 3 |
| OM |
| ON |
| OC |
分析:(1)利用椭圆的定义判断点P的轨迹 是以A、F 为焦点的椭圆,求出a、b的值,即得椭圆的方程.
(2)先假设存在一点C并设出坐标,以及设出M,N的坐标,根据向量共线得出x0=
,y0=
,然后联立直线方程和椭圆方程,得出x1+x2,y1+y2,进而得出x0=-
,
=
,求出m的值,即可求出C的坐标.
(2)先假设存在一点C并设出坐标,以及设出M,N的坐标,根据向量共线得出x0=
| x1+x2 |
| m |
| y1+y 2 |
| m |
8
| ||
| 15m |
| y | 0 |
| 2 |
| 5m |
解答:解:(1)由题意|PA|=|PB|,且|PB|+|PF|=8,
∴|PA|+|PF|=8>|AF|.
因此点P的轨迹是以A,F为焦点的椭圆.(4分)
设所求椭圆的方程为
+
=1(a>b>0),
∴2a=8,a=4,a2-b2=c2=22=4∴b2=12
∴点P的轨迹方程为
+
=1.(6分)
(2)假设存在满足题意的点C(x0,y0)(x0<0,y0>0),设M(x1,y1),N(x2,y2),
+
=m
(m∈R,且m≠0),
则(x1+x2,y1+y2)=m(x0,y0).
∴x0=
,y0=
.
由
,得15x2+8
x-44=0.(8分)
∴x1+x2=-
,y1+y2=
(x1+x2)+2=
.∴x0=-
,
=
.(10分)
又
+
=1,解得m2=
.∴m=±
.
又∵x0<0,y0>0
∴m=
所以存在满足题意的点C(-
,
)(14分)
∴|PA|+|PF|=8>|AF|.
因此点P的轨迹是以A,F为焦点的椭圆.(4分)
设所求椭圆的方程为
| x2 |
| a2 |
| y2 |
| b2 |
∴2a=8,a=4,a2-b2=c2=22=4∴b2=12
∴点P的轨迹方程为
| x2 |
| 16 |
| y2 |
| 12 |
(2)假设存在满足题意的点C(x0,y0)(x0<0,y0>0),设M(x1,y1),N(x2,y2),
| OM |
| ON |
| OC |
则(x1+x2,y1+y2)=m(x0,y0).
∴x0=
| x1+x2 |
| m |
| y1+y2 |
| m |
由
|
| 3 |
∴x1+x2=-
8
| ||
| 15 |
| 3 |
| 2 |
| 5 |
8
| ||
| 15m |
| y | 0 |
| 2 |
| 5m |
又
| ||
| 16 |
| ||
| 12 |
| 1 |
| 15 |
| ||
| 15 |
又∵x0<0,y0>0
∴m=
| ||
| 15 |
所以存在满足题意的点C(-
8
| ||
| 5 |
2
| ||
| 5 |
点评:本题考查了椭圆的定义以及直线与圆锥曲线问题,(1)问的关键是灵活掌握椭圆的定义.属于难题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
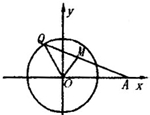 如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.
如图,已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当Q点在圆上移动时,求动点M的轨迹方程.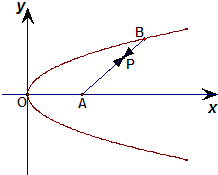 如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得
如图,已知定点A(2,0)及抛物线y2=x,点B在该抛物线上,若动点P使得