题目内容
(本小题满分12分)
已知向量 与
与 共线,且有函数
共线,且有函数
(Ⅰ)求函数 的周期与最大值;
的周期与最大值;
(Ⅱ)已知锐角DABC的三个内角分别是A、B、C,若有 ,边
,边 ,
, ,求AC的长.
,求AC的长.
【答案】
(1)f(x)的周期为2π,函数的最大值为2;(2)2.
【解析】
试题分析:∵向量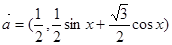 与
与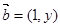 共线,
共线,
∴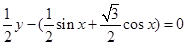 ,∴y=f(x)=
,∴y=f(x)=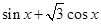 =2sin(
=2sin(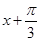 )
)
(Ⅰ)∵ω=1,∴T=2π,
∵-2≤2sin(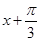 )≤2,s所以f(x)的周期为2π,函数的最大值为2;
)≤2,s所以f(x)的周期为2π,函数的最大值为2;
(Ⅱ)由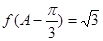 ,得2sin(
,得2sin( )=
)= ,即sinA=
,即sinA=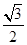 ,
,
∵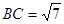 ,
,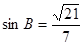 ,
,
∴由正弦定理
 得:AC=
得:AC=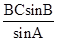 =2.
=2.
考点:本题主要考查平面向量的坐标运算,共线向量,两角和差的正弦,正弦函数的性质,正弦定理的应用。
点评:中档题,本题将平面向量、三角函数、正弦定理结合在一起进行考查,具有较强的综合性。本题解法体现的的是解答此类题的一般方法,如,研究三角函数的图象和性质,往往要先“化一”,研究三角形问题,往往利用正弦定理、余弦定理等等。

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目